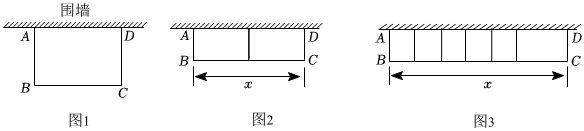
如图1,用篱笆靠墙围成矩形花圃ABCD,墙可利用的最大长度为15m,一面利用旧墙,其余三面用篱笆围,篱笆总长为24m,设平行于墙的BC边长为xm.
(1)若围成的花圃面积为40m2时,求BC的长;
(2)如图2,若计划在花圃中间用一道篱笆隔成两个小矩形,且围成的花圃面积为50m2,请你判断能否成功围成花圃,如果能,求BC的长?如果不能,请说明理由;
(3)如图3,若计划在花圃中间用n道篱笆隔成小矩形,且当这些小矩形为正方形时,请列出x、n满足的关系式 24-xn+2=xn+124-xn+2=xn+1.
24
-
x
n
+
2
=
x
n
+
1
24
-
x
n
+
2
=
x
n
+
1
【答案】
24
-
x
n
+
2
=
x
n
+
1
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/13 0:0:1组卷:2387引用:15难度:0.5
相似题
-
1.某药品,原来每盒售价96元,由于两次降价,现在每盒售价54元,平均每次降价的百分率是 %.
发布:2025/6/23 23:0:10组卷:104引用:23难度:0.7 -
2.已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.发布:2025/6/23 23:0:10组卷:12221引用:144难度:0.7 -
3.端午节期间,某品牌粽子经销商销售甲、乙两种不同味道的粽子,已知一个甲种粽子和一个乙种粽子的进价之和为10元,每个甲种粽子的利润是4元,每个乙种粽子的售价比其进价的2倍少1元,小王同学买4个甲种粽子和3个乙种粽子一共用了61元.
(1)甲、乙两种粽子的进价分别是多少元?
(2)在(1)的前提下,经销商统计发现:平均每天可售出甲种粽子200个.如果将甲种粽子的售价提高1元,则每天将少售出50个甲种粽子.现经销商决定把甲种粽子的价格提高x元,在不考虑其他因素的条件下,当x为多少元时,才能使该经销商每天销售甲种粽子获取的利润为350元?发布:2025/6/24 13:30:1组卷:61引用:1难度:0.3


