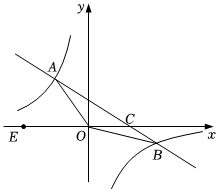
如图，在平面直角坐标系中，一次函数y1=kx+b（k≠0）的图象与反比例函数y2=mx（m≠0）的图象交于二、四象限内的A、B两点，与x轴交于C点，点B的坐标为（n,-2），线段OA=5，E为x轴负半轴上一点，且sin∠AOE=45．
（1）求该反比例函数和一次函数的解析式．
（2）求△AOB的面积．
（3）在反比例函数图象上找一点D，使△ABD的面积等于△AOB的面积，请直接写出点D的坐标．
y
2
=
m
x
（
m
≠
0
）
sin
∠
AOE
=
4
5
【考点】反比例函数与一次函数的交点问题．
【答案】（1）反比例函数解析式为y=-，一次函数解析式为y=-x+2；
（2）S△AOB=9；
（3）D1（-3，2），D2（3，2），D3（3-3，2+2），D4（3+3，2-2）．
12
x
2
3
（2）S△AOB=9；
（3）D1（-3
2
2
2
2
3
3
3
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/10 8:0:8组卷：140引用：1难度：0.4
相似题
-
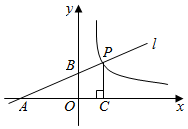1．如图，直线l：y=ax+b分别与x轴，y轴相交于A，B，与反比例函数y=（x＞0）的图象相交于点P（2，3），作PC⊥x轴于C，已知△APC的面积为9．kx
（1）请分别求出直线l与反比例函数y=的表达式；kx
（2）将直线l向下平移，平移后的直线与x轴相交于点D，与反比例函数y=（x＞0）的图象交于点Q，作QE⊥x轴于E，如果△APC的面积是△DEQ的面积的2倍，求点D的坐标．kx发布：2025/5/25 20:30:1组卷：891引用：3难度：0.6 -
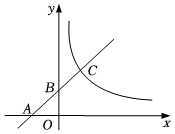2．如图，一次函数y=x+b（b＞0）的图象与x轴交于点A，与y轴交于点B，与反比例函数的图象交于点C，若AB=BC，则b的值为 ．y=8x发布：2025/5/25 20:30:1组卷：213引用：3难度：0.6 -
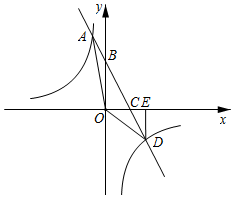3．如图，直线y=kx+3与x轴、y轴分别交于点B、C，与反比例函数y=交于点A、D，过D作DE⊥x轴于E，连接OA，OD，若A（-2，n），S△OAB：S△ODE=1：2．mx
（1）求反比例函数的表达式；
（2）求点C的坐标．发布：2025/5/25 20:30:1组卷：510引用：2难度：0.7
