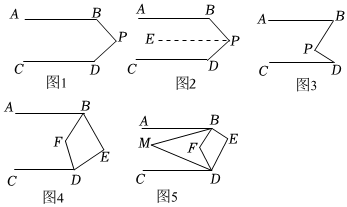
问题情境1：如图1，AB∥CD，P是AB、CD内部一点，P在BD的右侧，我们称这种模型为“铅笔模型”，探究∠B，∠P，∠D之间的关系，小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠B，∠P，∠D之间的关系是 ∠B+∠BPD+∠D=360°∠B+∠BPD+∠D=360°；
问题情境2：如图3，AB∥CD，P是AB，CD内部一点，P在BD的左侧，我们称这种模型为“猪脚模型”，仿照问题1的思路可得∠B，∠P，∠D之间的关系是 ∠BPD=∠B+∠D∠BPD=∠B+∠D；
问题迁移：请合理利用上面的结论解决以下问题：
已知AB∥CD，∠ABE与∠CDE两个角的角平分线相交于点F．
（1）如图4，若∠E=80°，求∠BFD的度数；
（2）如图5中，∠ABM=13∠ABF，∠CDM=13∠CDF，探究∠M与∠E之间的数量关系；
（3）如图5中，若∠ABM=1n∠ABF，∠CDM=1n∠CDF，设∠E=m°，用含有n,m°的代数式直接写出∠M=360°-m°2n360°-m°2n．
∠
ABM
=
1
3
∠
ABF
∠
CDM
=
1
3
∠
CDF
∠
ABM
=
1
n
∠
ABF
∠
CDM
=
1
n
∠
CDF
360
°
-
m
°
2
n
360
°
-
m
°
2
n
【考点】平行线的性质．
【答案】∠B+∠BPD+∠D=360°；∠BPD=∠B+∠D；
360
°
-
m
°
2
n
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/6 8:0:9组卷：821引用：1难度：0.3
相似题
-
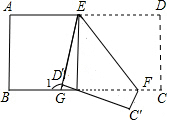1．如图，将一张长方形纸片沿EF折叠后，点D、C分别落在点D′、C′的位置，ED′的延长线与BC相交于点G，若∠EFG=50°，则∠1为（ ）发布：2025/6/25 7:30:2组卷：251引用：1难度：0.5 -
2．如图1，AD∥BC，∠BAD的平分线交BC于点G，∠BCD=90°．
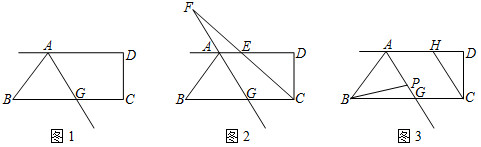
（1）求证：∠BAG=∠BGA；
（2）如图2，若∠ABG=50°，∠BCD的平分线交AD于点E、交射线GA于点F．求∠AFC的度数；
（3）如图3，线段AG上有一点P，满足∠ABP=3∠PBG，过点C作CH∥AG．若在直线AG上取一点M，使∠PBM=∠DCH，请直接写出的值．∠ABM∠GBM发布：2025/6/25 7:30:2组卷：2779引用：11难度：0.5 -
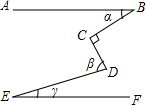3．如图，AB∥EF，∠C=90°，则α、β、γ的关系为（ ）发布：2025/6/25 7:0:2组卷：5732引用：29难度：0.7
