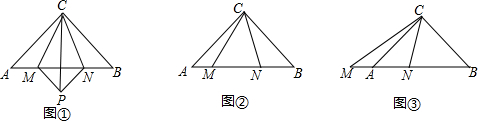
如图①，等腰三角形ABC中，∠BCA=90°，AC=CB，点M、N在边AB上，且∠MCN=45°．
（1）如图①，当AM=BN时，将△ACM沿CM折叠，点A落在P处，再将△BCN沿CN折叠，点B也恰好落在P点处，此时，PM=AM，PN=BN，△PMN的形状是 等腰直角三角形等腰直角三角形，线段AM、BN、MN之间的关系是 AM2+BN2=MN2（或AM=BN=22MN）AM2+BN2=MN2（或AM=BN=22MN）；
（2）如图②，∠MCN绕点C在∠ACB内部任意位置时，线段MN、AM、BN之间的数量关系是 AM2+BN2=MN2AM2+BN2=MN2．试证明你的猜想：若AM=1，BN=3，求MN的长．
（3）当∠MCN图③的位置时，线段MN、AM、BN之间的数量关系是 AM2+MN2=BN2AM2+MN2=BN2．（不要求证明）
2
2
2
2
【考点】几何变换综合题．
【答案】等腰直角三角形；AM2+BN2=MN2（或AM=BN=MN）；AM2+BN2=MN2；AM2+MN2=BN2
2
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/20 15:0:2组卷：341引用：3难度：0.3
相似题
-
1．如图1，AB，BC被直线AC所截，∠B=72o，∠BAC＜∠B，过点A作AE∥BC，点D是线段AC上的点，过点D作DE∥AB交AE于点E．
（1）填空：∠E=；
（2）将线段AE沿线段AC方向平移得到线段PQ，连接DQ．
①如图2，当∠EDQ=45°时，求∠Q的度数；
②如图3，当∠EDQ=90°时，则∠Q=；
③在整个平移过程中，是否存在∠EDQ=3∠Q，若存在，直接写出此时∠Q的度数，若不存在说明理由．
发布：2025/6/5 6:30:2组卷：108引用：2难度：0.2 -
2．【问题背景】
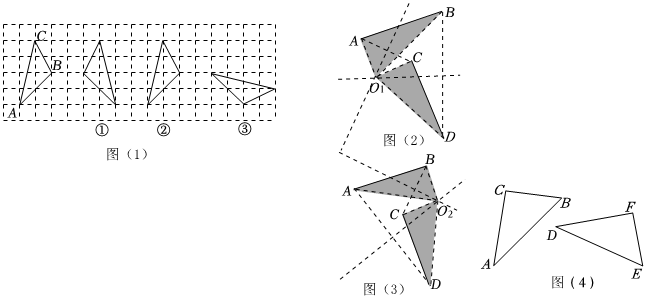
在图（1）中，①～③的三个三角形，各自是由△ABC通过怎样的全等变换得到的？
【问题探究】
（1）我们发现：
Ⅰ：图（1）中，①号三角形能由△ABC通过一次轴对称得到，请在图（1）中画出对称轴．
Ⅱ：图（1）中，②号三角形能由△ABC通过一次平移得到，则平移的距离为 单位．
Ⅲ：图（1）中，③号三角形能由△ABC通过先平移再旋转或先旋转再平移得到，请问：③号三角形能否由△ABC绕某个点，旋转一次得到？为解决这个问题，我们可以先解决两条相等的线段能否看成：一条线段是另一条线段绕某个点旋转一次得到．分析过程如下：
已知线段AB与线段CD相等，分两种情况讨论：
第一种情况：当AB与CD对应时，如图（2），分别作AC与BD的中垂线交于点O1，连接O1A、O1C、O1B、O1D．
∵O1在AC的中垂线上
∴O1A=O1C
同理，O1B=O1D
又∵AB=CD
∴△ABO1≌△CDO1（SSS）
∴∠AO1B=∠CO1D
∴∠AO1C=∠BO1D，即对应点与点O1形成的夹角相等
∴线段CD可以看成由线段AB绕点O1旋转一次得到.
第二种情况：当AB与DC对应时，如图（3），同理可证．
综上所述：两条相等的线段可以看成：一条线段是另一条线段绕某个点旋转一次得到．
【问题解决】
（2）如图（4），已知△ABC≌△DEF（且满足△DEF不能由△ABC通过平移得到）．现在来解决△DEF能由△ABC绕某个点通过一次旋转得到的问题：
①通过尺规作图找到旋转中心O；
②证明：△DEF能由△ABC绕点O通过一次旋转得到．（提示：只要证明关键的对应点到点O的距离相等和关键的对应点与点O形成的夹角相等）发布：2025/6/5 6:0:2组卷：367引用：5难度：0.2 -
3．已知△ABC是边长为4的等边三角形，点D是射线BC上的动点，将线段AD绕点D顺时针方向旋转60°得到线段DE，连接CE．
（1）如图1，求证：CE=BD；
（2）①当BD=时，∠DEC=30°；（直接写出结果）
②点D在运动过程中，△DEC的周长是否存在最小值？若存在，请直接写出△DEC周长的最小值；若不存在，请说明理由．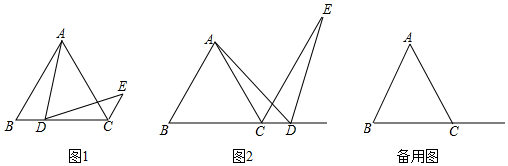
发布：2025/6/5 5:30:2组卷：444引用：3难度：0.2
