古希腊数学家帕普斯在《数学汇编》第三卷中记载着一个确定重心的定理：“如果同一平面内的一个闭合图形的内部与一条直线不相交，那么该闭合图形围绕这条直线旋转一周所得到的旋转体的体积等于闭合图形面积乘以该闭合图形的重心旋转所得周长的积”，即V=Sl（V表示平面图形绕旋转轴旋转的体积，S表示平面图形的面积，l表示重心绕旋转轴旋转一周的周长）．已知Rt△ACB中，AB⊥AC，AB=2，AC=4，则△ACB的重心G到AC的距离为（ ）
【考点】旋转体（圆柱、圆锥、圆台）的体积．
【答案】B
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：82引用：3难度：0.6
相似题
-
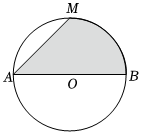1．如图，AB是圆O的直径，点M是的中点．若AB=2，则图中阴影部分绕AB所在直线旋转一周形成的几何体的表面积等于 ．ˆAB发布：2025/1/20 8:0:1组卷：110引用：2难度：0.7 -
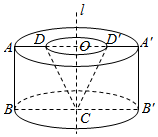2．如图，梯形ABCD中，AD∥BC，∠ABC=90°，AD=a,BC=2a,∠DCB=60°，在平面ABCD内过点C作l⊥CB，以l为轴旋转一周．求旋转体的表面积和体积．发布：2024/12/29 9:30:1组卷：160引用：8难度：0.5 -
3．圆锥的高为1，体积为π，则过该圆锥顶点的平面截此圆锥所得截面面积的最大值为（ ）
发布：2024/12/29 20:30:4组卷：266引用：9难度：0.8
