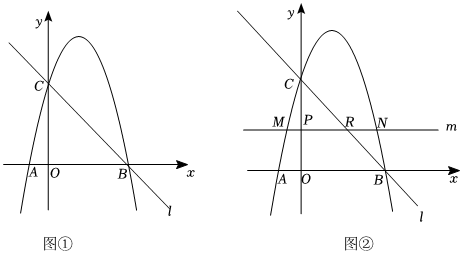
如图①，二次函数y=-x2+bx+c的图象与x轴交于A、B两点，与y轴交于点C．点B的坐标为（4，0），点C的坐标为（0，4），直线l经过B、C两点．
（1）b=33，c=44．
（2）点P为y轴上的动点，过点P且平行于x轴的直线m,分别交该二次函数的图象于点M、N（点M在点N的左边），交直线l于点R（如图②）．
①当点R为线段MN的中点时，求N点的坐标．
②设M、N、R的横坐标分别x1，x2，x3，点P的纵坐标为t.若（x1-x3）（x2-x3）＞0，则t的取值范围是 4＜t＜254或t＜04＜t＜254或t＜0．
（3）若将该二次函数的图象进行适当平移，当平移后的图象与直线l最多只有一个公共点时，请直接写出图象平移的最短距离，并求出平移后的二次函数图象的顶点坐标．
25
4
25
4
【考点】二次函数综合题．
【答案】3；4；4＜t＜或t＜0
25
4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/30 8:0:9组卷：173引用：1难度：0.1
相似题
-
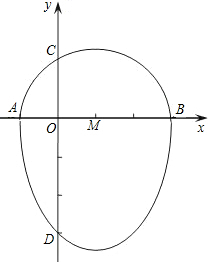1．我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线．如图所示，点A、B、C、D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为（0，-3），AB为半圆的直径，半圆圆心M的坐标为（1，0），半圆半径为2．
（1）请你求出“蛋圆”抛物线部分的解析式，并写出自变量的取值范围；
（2）你能求出经过点C的“蛋圆”切线的解析式吗？试试看；
（3）开动脑筋想一想，相信你能求出经过点D的“蛋圆”切线的解析式．发布：2025/6/8 14:30:2组卷：237引用：45难度：0.1 -
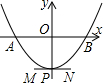2．如图，一条抛物线与x轴相交于A、B两点（点A在点B的左侧），其顶点P在线段MN上移动．若点M、N的坐标分别为（-1，-2）、（1，-2），点B的横坐标的最大值为3，则点A的横坐标的最小值为（ ）发布：2025/6/8 8:0:6组卷：4103引用：19难度：0.7 -
3．已知函数y=
，记该函数图象为G．-12x2+12x+m（x＜m）x2-mx+m（x≥m）
（1）当m=2时，
①已知M（4，n）在该函数图象上，求n的值；
②当0≤x≤2时，求函数G的最大值．
（2）当m＞0时，作直线x=m与x轴交于点P，与函数G交于点Q，若∠POQ=45°时，求m的值；12
（3）当m≤3时，设图象与x轴交于点A，与y轴交于点B，过点B作BC⊥BA交直线x=m于点C，设点A的横坐标为a,C点的纵坐标为c,若a=-3c,求m的值．发布：2025/6/8 14:30:2组卷：3081引用：7难度：0.1
