勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当两个全等的直角三角形如图①或图②摆放时,都可以用“面积法”来证明,下面是小明利用图①证明勾股定理的过程:将两个全等的直角三角形按图①所示摆放,其中∠DAB=90°,求证:a2+b2=c2.

证明:连接DB,过点D作BC边上的高DF,则DF=EC=b-a,FC=DE=b,
∵S四边形ADCB=S△ACD+S△ABC=12b2+12ab,
S四边形ADCB=S△ADB+S△DCB=12c2+12a(b-a)
∴12b2+12ab=12c2+12a(b-a)
∴a2+b2=c2.
请参照上述证法,利用图②完成下面的证明:
将两个全等的直角三角形按图②所示摆放,其中∠DAB=90°.求证:a2+b2=c2.
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
【考点】勾股定理的证明;直角三角形全等的判定.
【答案】见解答.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/20 7:0:2组卷:226引用:1难度:0.7
相似题
-
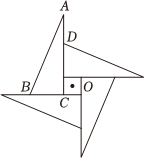 1.10.《时代数学学习》杂志2007年3月将改版为《时代学习报•数学周刊》,其徽标是我国古代“弦图”的变形(见示意图).该图可由直角三角形ABC绕点O同向连续旋转三次(每次旋转90°)而得.因此有“数学风车”的动感.假设中间小正方形的面积为1,整个徽标(含中间小正方形)的面积为92,AD=2,则徽标的外围周长为( )发布:2025/1/25 8:0:2组卷:363引用:2难度:0.6
1.10.《时代数学学习》杂志2007年3月将改版为《时代学习报•数学周刊》,其徽标是我国古代“弦图”的变形(见示意图).该图可由直角三角形ABC绕点O同向连续旋转三次(每次旋转90°)而得.因此有“数学风车”的动感.假设中间小正方形的面积为1,整个徽标(含中间小正方形)的面积为92,AD=2,则徽标的外围周长为( )发布:2025/1/25 8:0:2组卷:363引用:2难度:0.6 -
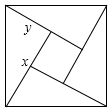 2.用四个全等的直角三角形镶嵌而成的正方形如图所示,已知大正方形的面积为49,小正方形的面积为4,若x,y表示直角三角形的两直角边长(x>y),给出下列四个结论正确的是 .(填序号即可)
2.用四个全等的直角三角形镶嵌而成的正方形如图所示,已知大正方形的面积为49,小正方形的面积为4,若x,y表示直角三角形的两直角边长(x>y),给出下列四个结论正确的是 .(填序号即可)
①x-y=2;
②x2+y2=49;
③2xy=45;
④x+y=9.发布:2024/12/23 12:0:2组卷:459引用:3难度:0.6 -
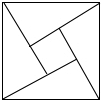 3.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为( )发布:2024/12/19 23:30:5组卷:1867引用:29难度:0.6
3.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为( )发布:2024/12/19 23:30:5组卷:1867引用:29难度:0.6


