规律探究：
15×15=1×2×100+25=225；
25×25=2×3×100+25=625；
35×35=3×4×100+25=1225；
（1）第4行为 45×45=4×5×100+25=202545×45=4×5×100+25=2025；
（2）用含n的式子表示规律并证明．
【考点】规律型：数字的变化类；列代数式．
【答案】45×45=4×5×100+25=2025
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/1 8:0:9组卷：69引用：6难度：0.7
相似题
-
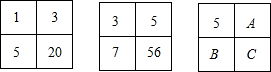
1．如图，填在下面三个田字格内的四个数具有相同的规律，根据此规律，则C=．
发布：2025/6/9 16:0:2组卷：158引用：30难度：0.5 -
2．先阅读理解，再回答下列问题：
因为=12+1，且1＜2＜2，所以2的整数部分为1；12+1
因为=22+2，且2＜6＜3，所以6的整数部分为2；22+2
因为=32+3，且3＜12＜4，所以12的整数部分为3；32+3
（1）以此类推，我们会发现（n为正整数）的整数部分为 ；请说明理由；n2+n
（2）已知的整数部分为a,20的整数部分为b,求a+b的值．132发布：2025/6/9 11:0:1组卷：29引用：1难度：0.6 -
3．观察下列算式：152=225，252=625，352=1225，452=2025…．
（1）可猜想；752=；
（2）若用正整数n表示（1）中等号左边的两位数中的十位数字，则可用含n的等式表示（1）的运算规律：；
（3）请用所学知识说明（2）所写等式的正确性．发布：2025/6/9 13:0:1组卷：39引用：2难度：0.7
