如图1,把一副直角三角板的直角边BO和DO分别放在直线MN上,两个三角板分别在直线MN两侧,∠AOB=90°,∠COD=30°.
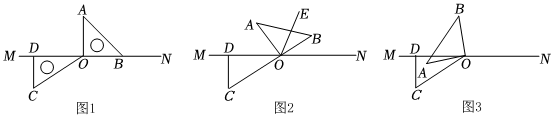
(1)在图1中,∠AOC=120°120°,∠BOC=150°150°;
(2)如图2,OE为射线,将三角板AOB绕点O旋转,使△AOB的一边OB恰好平分∠NOE.问:此时OA是否平分∠DOE?请说明理由;
(3)将图2中的三角板AOB绕点O旋转至图3的位置,使OA在∠DOC的内部.
①求∠COB+∠DOA的度数;
②求∠BOD-∠AOC的度数.
【考点】余角和补角.
【答案】120°;150°
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/27 10:35:59组卷:843引用:4难度:0.6
相似题
-
1.如图,将两个直角三角板的顶点叠放在一起进行探究.

(1)如图①,将一副直角三角板的直角顶点C叠放在一起,若CE恰好是∠ACB的平分线,请你猜想此时CB是不是∠ECD的平分线,并简述理由;
(2)如图②,将一副直角三角板的直角顶点C叠放在一起,若CB始终在∠DCE的内部,请猜想∠ACE与∠DCB是否相等,并简述理由.发布:2025/6/8 2:30:2组卷:125引用:3难度:0.5 -
2.若一个角的补角是43°,则这个角的度数为.
发布:2025/6/8 2:30:2组卷:155引用:7难度:0.9 -
3.若∠1与∠2互补,∠2与30°互余,则∠1=度.
发布:2025/6/8 7:0:2组卷:352引用:4难度:0.7


