祖暅是我国南北朝时期伟大的数学家．祖暅原理用现代语言可以描述为“夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的面积总相等，那么这两个几何体的体积相等．”例如可以用祖暅原理推导半球的体积公式，如图，底面半径和高都为R的圆柱与半径为R的半球放置在同一底平面上，然后在圆柱内挖去一个半径为R，高为R的圆锥后得到一个新的几何体，用任何一个平行于底面的平面α去截这两个几何体时，所截得的截面面积总相等，由此可证明半球的体积和新几何体的体积相等．若用垂直于半径的平面α去截半径为R的半球，且球心到平面α的距离为12R，则平面α所截得的较小部分（阴影所示称之为“球冠）的几何体的体积是（ ）
1
2
R
【考点】棱柱、棱锥、棱台的体积；球的体积和表面积．
【答案】A
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：245引用：3难度：0.6
相似题
-
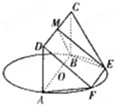1．如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD的边BC垂直于圆O所在的平面，且AB=2，AD=EF=1．
（Ⅰ）设CD的中点为M，求证：EM∥平面DAF；
（Ⅱ）求三棱锥B-CME的体积．发布：2025/1/20 8:0:1组卷：16引用：1难度：0.5 -
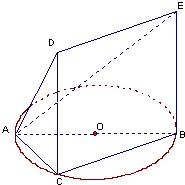2．如图，△ABC内接于圆O，AB是圆O的直径，AB=2，BC=1，设AE与平面ABC所成的角为θ，且tanθ=，四边形DCBE为平行四边形，DC⊥平面ABC．32
（1）求三棱锥C-ABE的体积；
（2）证明：平面ACD⊥平面ADE；
（3）在CD上是否存在一点M，使得MO∥平面ADE？证明你的结论．发布：2025/1/20 8:0:1组卷：95引用：3难度：0.1 -
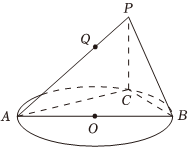3．如图所示，AB为圆O的直径，PC⊥平面ABC，Q在线段PA上．
（1）求证：平面BCQ⊥平面ACQ；
（2）若Q为靠近P的一个三等分点，PC=BC=1，，求VP-BCQ的值．AC=22发布：2025/1/20 8:0:1组卷：37引用：3难度：0.6
