甲、乙两个袋子里各有1个白球和1个黑球，每次独立地从两个袋子中随机取出1个球相互交换后放回袋中，若第n次交换后，甲袋中两个球颜色相同，记Xn=1，否则，Xn=0．
（1）求X1=0 的概率；
（2）求Xn=1 的概率；
（3）记Y=n∑i=1Xi，求E（Y）．
n
∑
i
=
1
【考点】离散型随机变量的均值（数学期望）．
【答案】（1）．
（2）．
（3）．
1
2
（2）
1
3
+
1
6
（
-
1
2
）
n
-
1
（3）
n
3
+
1
9
[
1
-
（
-
1
2
）
n
]
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/17 2:0:1组卷：38引用：1难度：0.5
相似题
-
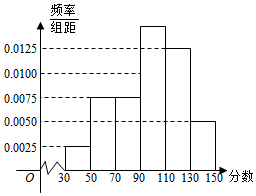1．某市举行“中学生诗词大赛”，分初赛和复赛两个阶段进行，规定：初赛成绩大于90分的具有复赛资格，某校有800名学生参加了初赛，所有学生的成绩均在区间（30，150]内，其频率分布直方图如图．
（Ⅰ）求获得复赛资格的人数；
（Ⅱ）从初赛得分在区间（110，150]的参赛者中，利用分层抽样的方法随机抽取7人参加学校座谈交流，那么从得分在区间（110，130]与（130，150]各抽取多少人？
（Ⅲ）从（Ⅱ）抽取的7人中，选出3人参加全市座谈交流，设X表示得分在区间（130，150]中参加全市座谈交流的人数，求X的分布列及数学期望E（X）．发布：2024/12/29 13:30:1组卷：133引用：7难度：0.5 -
2．设离散型随机变量X的分布列如表：
若离散型随机变量Y=-3X+1，且E（X）=3，则（ ）X 1 2 3 4 5 P m 0.1 0.2 n 0.3 发布：2024/12/29 13:0:1组卷：195引用：6难度：0.5 -
3．从4名男生和2名女生中任选3人参加演讲比赛，用X表示所选3人中女生的人数，则E（X）为（ ）
发布：2024/12/29 13:30:1组卷：137引用：6难度：0.7
