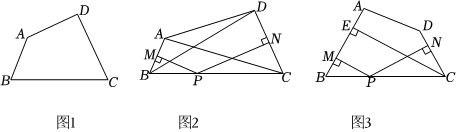
我们给出如下定义：有一组邻角相等的凸四边形叫做“等邻角四边形”．例如：如图1，∠B=∠C，则四边形ABCD为等邻角四边形．
（1）定义理解：以下平面图形中，一定是等邻角四边形的是 ②④②④；
①平行四边形；②矩形；③菱形；④正方形．
（2）如图2，在四边形ABCD中，AB，CD的垂直平分线恰好交于BC边上一点P，连接AC，BD，且AC=BD，求证：四边形ABCD为等邻角四边形；
（3）如图3，在等邻角四边形ABCD中，∠B=∠BCD，CE⊥AE，点P为边BC上的一动点，过点P作PM⊥AB，PN⊥CD，垂足分别为M，N．在点P的运动过程中，猜想PM，PN，CE之间的数量关系？并请说明理由．
【考点】四边形综合题．
【答案】②④
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/16 8:0:10组卷：74引用：2难度：0.3
相似题
-
1．如图，在平面直角坐标系中，矩形ABCD的边AB在x轴上，AB、BC的长分别是一元二次方程x2-7x+12=0的两个根（BC＞AB），OA=2OB，边CD交y轴于点E，动点P以每秒1个单位长度的速度，从点E出发沿折线段ED-DA向点A运动，运动的时间为t（0≤t＜6）秒，设△BOP与矩形AOED重叠部分的面积为S．
（1）求点D的坐标；
（2）求S关于t的函数关系式，并写出自变量的取值范围；
（3）在点P的运动过程中，是否存在点P，使△BEP为等腰三角形？若存在，直接写出点P的坐标；若不存在，请说明理由．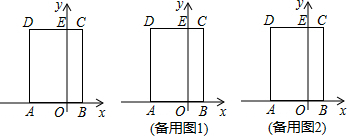
发布：2025/5/23 3:30:1组卷：862引用：5难度：0.4 -
2．已知：菱形ABCD和菱形A′B′C′D′，∠BAD=∠B′A′D′，起始位置点A在边A′B′上，点B在A′B′所在直线上，点B在点A的右侧，点B′在点A′的右侧，连接AC和A′C′，将菱形ABCD以A为旋转中心逆时针旋转α角（0°＜α＜180°）．
（1）如图1，若点A与A′重合，且∠BAD=∠B′A′D′=90°，求证：BB′=DD′．
（2）若点A与A′不重合，M是A′C′上一点，当MA′=MA时，连接BM和A′C，BM和A′C所在直线相交于点P．
①如图2，当∠BAD=∠B′A′D′=90°时，请猜想线段BM和线段A′C的数量关系及∠BPC的度数．
②如图3，当∠BAD=∠B′A′D′=60°时，请求出线段BM和线段A′C的数量关系及∠BPC的度数．
③在②的条件下，若点A与A′B′的中点重合，A′B′=4，AB=2，在整个旋转过程中，当点P与点M重合时，请直接写出线段BM的长．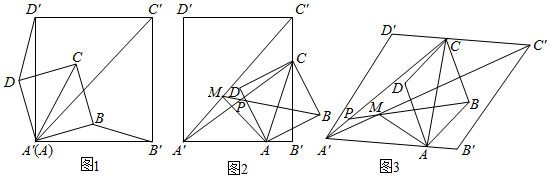
发布：2025/5/23 3:30:1组卷：1720引用：3难度：0.1 -
3．【推理】
如图1，在边长为10的正方形ABCD中，点E是CD上一动点，将正方形沿着BE折叠，点C落在点F处，连结BE，CF，延长CF交AD于点G，BE与CG交于点M．
（1）求证：CE=DG．
【运用】
（2）如图2，在【推理】条件下，延长BF交AD于点H．若CE=6，求线段DH的长．
【拓展】
（3）如图3，在【推理】条件下，连结AM．则线段AM的最小值为 ．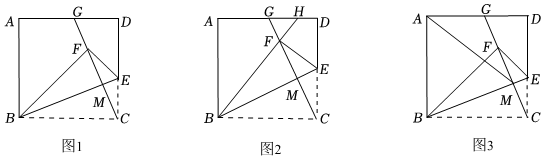
发布：2025/5/23 4:0:1组卷：423引用：5难度：0.4
