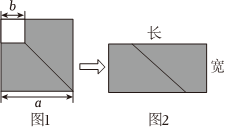
如图1，边长为a的大正方形内有一个边长为b的小正方形．
（1）用含字母的代数式表示图1中阴影部分的面积为 a2-b2a2-b2；
（2）将图1的阴影部分沿斜线剪开后，拼成了一个如图2所示的长方形，用含字母的代数式表示此长方形的面积为 （a+b）（a-b）（a+b）（a-b）；（多项式乘积的形式）
（3）比较图1和图2的阴影部分面积，请你写出一个整式乘法的公式 （a+b）（a-b）=a2-b2（a+b）（a-b）=a2-b2；
（4）结合（3）的公式，计算：①（x-2）（x+2）（x2+4）；
②（1+12）（1+122）（1+124）（1+128）+1215；
【拓展】：直接写出（2+1）（22+1）（24+1）（28+1）…（232+1）+1结果的个位数字．
（
1
+
1
2
）
（
1
+
1
2
2
）
（
1
+
1
2
4
）
（
1
+
1
2
8
）
+
1
2
15
【考点】平方差公式的几何背景；尾数特征．
【答案】a2-b2；（a+b）（a-b）；（a+b）（a-b）=a2-b2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/23 10:0:9组卷：129引用：2难度：0.5
相似题
-
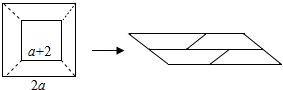1．如图，在边长为2a的正方形中央剪去一边长为（a+2）的小正方形（a＞2），将剩余部分剪开密铺成一个平行四边形，则该平行四边形的面积为（ ）发布：2025/6/24 0:0:1组卷：7411引用：77难度：0.7 -
2．乘法公式的探究及应用．
（1）如图1，可以求出阴影部分的面积是（写成两数平方差的形式）；
（2）如图2，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是，长是，面积是（写成多项式乘法的形式）；
（3）比较左、右两图的阴影部分面积，可以得到乘法公式（用式子表达）．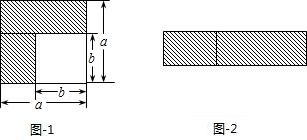
发布：2025/6/24 11:30:1组卷：748引用：18难度：0.7 -
3．如图，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分的面积，验证了公式 ．发布：2025/6/24 1:0:1组卷：1937引用：58难度：0.7
