某校积极开展社团活动，在一次社团活动过程中，一个数学兴趣小组发现《九章算术》中提到了“刍薨”这个五面体，于是他们仿照该模型设计了一道数学探究题，如图1，E、F、G分别是边长为4的正方形的三边AB、CD、AD的中点，先沿着虚线段FG将等腰直角三角形FDG裁掉，再将剩下的五边形ABCFG沿着线段EF折起，连接AB、CG就得到了一个“刍甍”（如图2）．
（1）若O是四边形EBCF对角线的交点，求证：AO∥平面GCF；
（2）若二面角A-EF-B的大小为23π，求平面OAB与平面ABE夹角的余弦值．
2
3
π
【考点】二面角的平面角及求法；直线与平面平行．
【答案】（1）AO∥平面GCF．
（2）．
（2）
17
17
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/5 8:0:8组卷：392引用：11难度：0.6
相似题
-
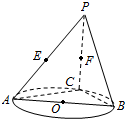1．如图，AB是圆O的直径，点C是圆O上异于A，B的点，直线PC⊥平面ABC，E，F分别是PA，PC的中点．
（Ⅰ）记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系，并加以证明；
（Ⅱ）设（Ⅰ）中的直线l与圆O的另一个交点为D，且点Q满足．记直线PQ与平面ABC所成的角为θ，异面直线PQ与EF所成的角为α，二面角E-l-C的大小为β．求证：sinθ=sinαsinβ．DQ=12CP发布：2025/1/20 8:0:1组卷：907引用：12难度：0.1 -
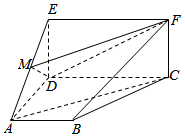2．如图，四边形ABCD为梯形，四边形CDEF为矩形，平面ABCD⊥平面CDEF，∠BAD=∠ADC=90°，AB=AD=DE=CD，M为AE的中点．12
（1）证明：AC∥平面MDF；
（2）求平面MDF与平面BCF的夹角的大小．发布：2025/1/2 8:0:1组卷：141引用：1难度：0.6 -
3．如图，AB是圆O的直径，PA垂直于圆所在的平面，C是圆周上的点．
（1）求证：平面PAC⊥平面PBC；
（2）若AB=2，AC=2，PA=2，求二面角C-PB-A的度数．2发布：2025/1/28 8:0:2组卷：33引用：1难度：0.5
