已知：如图，正方形ABCD中，点E是CD边上一点，作射线BE，过点D作DF⊥BE于点F，交BC的延长线于点G，连接FC．求证：BF-DF=2CF．
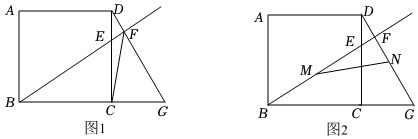
（1）小明和小颖根据题中的条件发现：图1中存在和∠EBC相等的角，即 ∠GDC=∠EBC∠GDC=∠EBC；
（2）在证明结论时，小明和小颖有了不同的思路．小颖：我受结论中“BF-DF”的启发，可在线段BF上截取BH=DF，再证HF=2CF…
小明，我受结论中“2CF”的启发，可构造一个以CF为直角边的等腰直角三角形…
请从小明和小颖的思路中任选一种作出辅助线并给出证明；
（3）老师对问题进行了拓展：如图2，点M，N分别是线段BE，DG的中点，若AB=4，DE=1，则MN的长度为 522522．
2
2
2
5
2
2
5
2
2
【考点】四边形综合题．
【答案】∠GDC=∠EBC；
5
2
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/30 8:0:9组卷：65引用：1难度：0.3
相似题
-
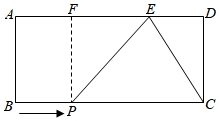1．如图，矩形ABCD中，AB=4，AD=8，E在AD上，DE=3，点P从点B出发，以每秒1个单位长度的速度沿着BC边向终点C运动，连接PE，设点P运动的时间为t秒．
（1）过P作PF⊥AD，垂足为F，用含t的式子表示：EF=，PC=；
（2）当t=2时，判断△PEC是否是直角三角形，并说明理由；
（3）当∠PEC=∠DEC时，求t的值．发布：2025/6/8 12:30:1组卷：43引用：3难度：0.4 -
2．如图，在正方形ABCD中，AB=BC=CD=AD=6，∠A=∠B=∠BCD=∠ADC=90°，将一直角三角板放在正方形ABCD上，使三角板的直角顶点与D点重合，三角板的一边交AB于点P，另一边交BC的延长线于点Q，如图1所示．
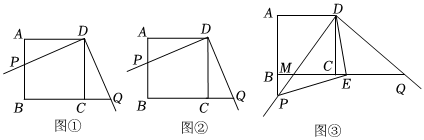
（1）求证：DP=DQ；
（2）如图2，在图1的基础上作∠PDQ的平分线DE交BC于点E，连接PE，请你猜想PE和QE存在何种数量关系，并予以证明；
（3）如图3，固定三角板直角顶点在D点不动，转动三角板使三角板的一边交AB的延长线于点P，另一边交BC的延长线于点Q，仍作∠PDQ的平分线DE交BC的延长线于点E，连接PE，若BP=2，求△DCE的面积．发布：2025/6/8 12:30:1组卷：58引用：1难度：0.2 -
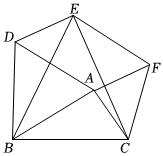3．（1）感知：如图，分别以△ABC的三边为边长，在BC边的同侧分别作三个等边三角形，即△ABD，△BCE，△ACF，连接DE、EF，试猜想四边形ADEF的形状，并证明你的猜想．
（2）应用：当△ABC中有AB=AC时，四边形ADEF的形状是 ．
（3）探究：①四边形ADEF是否随着△ABC形状的改变而永远存在，简要说明理由；
②如果四边形ADEF是正方形，则△ABC应满足什么条件？
（4）若AB=4，AC=3，BC=5，求四边形AFED的面积．发布：2025/6/8 12:30:1组卷：66引用：2难度：0.3
