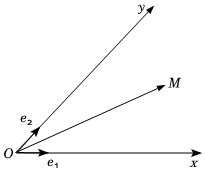
如图所示，设Ox,Oy是平面内相交成θ（θ≠π2）角的两条数轴，e1，e2分别是与x,y轴正方向同向的单位向量，则称平面坐标系xOy为θ斜坐标系，若OM=xe1+ye2，则把有序数对（x,y）叫做向量OM的斜坐标，记为OM=（x,y）．在θ=π4的斜坐标系中，a=（12，32），b=（3，-1）．则下列结论中，错误的是（ ）
①a-b=（12-3，32+1）；
②|a|=1；
③a⊥b；
④b在a上的投影为-2．
θ
（
θ
≠
π
2
）
e
1
，
e
2
OM
=
x
e
1
+
y
e
2
OM
OM
=
（
x
,
y
）
θ
=
π
4
a
=
（
1
2
，
3
2
）
，
b
=
（
3
，-
1
）
a
-
b
=
（
1
2
-
3
，
3
2
+
1
）
|
a
|
=
1
a
⊥
b
b
a
-
2
【答案】D
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/19 8:0:9组卷：25引用：2难度：0.8
