阅读下面的情景对话，然后解答问题：
老师：我们将奇异三角形定义为两边平方和等于第三边平方的2倍的三角形．
小华：等边三角形一定是奇异三角形!
小明：那直角三角形是否存在奇异三角形呢？
【感知】
（1）根据“奇异三角形”的定义，小红得出命题：“等边三角形一定是奇异三角形”，请判断小红提出的命题是否正确，并填空 正确正确（填“正确”或“不正确”）；
（2）若某三角形的三边长分别是3、11、7，则△ABC是奇异三角形吗？是是（填“是”或“不是”）；
【思考】
（1）若Rt△ABC是奇异三角形，且其两边长分别为2、23，则第三边的边长为 2222；且此直角三角形的三边之比为 1：2：31：2：3（请按从小到大排列）；
（2）如图1，在Rt△ABC中，∠ACB=90°，AB=c,AC=b,BC=a,且b＞a,若Rt△ABC是奇异三角形，求a：b：c；
【运用】如图2，在Rt△ABC中，∠ACB=90°，以AB为斜边作等腰直角△ABD，点E是AC下方的一点，且满足AE=AD，CE=CB．
（1）求证：△ACE是奇异三角形；
（2）当△ACE是直角三角形时，记△ABC的面积为S1，四边形ACBD的面积为S2，则S1S2=23-3．23-3．．
11
7
2
3
2
2
2
3
2
3
S
1
S
2
3
3
【考点】四边形综合题．
【答案】正确；是；2；1：：；2-3．
2
2
3
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/11 11:0:2组卷：346引用：2难度：0.4
相似题
-
1．如图，A、B、C、D为矩形的四个顶点，AB=6cm,AD=2cm,动点P、Q分别从点A、C同时出发，点P以2cm/s的速度向终点B移动，点Q以1cm/s的速度向终点D移动，当有一点到达终点时，另一点也停止运动．设运动时间为t求：
（1）当t=1s时，求四边形BCQP的面积？
（2）当t为何值时，点P与点Q之间的距离为cm？5
（3）当t=时，以点P，Q，D为顶点的三角形是等腰三角形．发布：2025/6/14 20:30:2组卷：182引用：4难度：0.3 -
2．综合与实践
问题情景：数学活动课上，老师出示了一个问题：如图①，在▱ABCD中，BE⊥AD，垂足为E，F为CD的中点，连接EF，BF，试猜想EF与BF的数量关系，并加以证明；
独立思考：（1）请解答老师提出的问题；
实践探究：（2）希望小组受此问题的启发，将▱ABCD沿着BF（F为CD的中点）所在直线折叠，如图②，点C的对应点为C'，连接DC'并延长交AB于点G，请判断AG与BG的数量关系，并加以证明；
问题解决：（3）智慧小组突发奇想，将▱ABCD沿过点B的直线折叠，如图③，点A的对应点A′，使A'B⊥CD于点H，连接A'M，交CD于点N，该小组提出一个问题：若此▱ABCD的面积为20，边长AB=5，BC=，求图中阴影部分（四边形BHNM）的面积．请你思考此问题，直接写出结果．833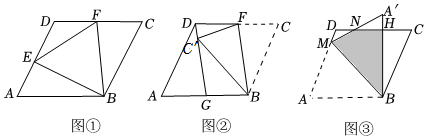
发布：2025/6/14 19:30:1组卷：200引用：1难度：0.1 -
3．（1）问题引入
如图1，点F是正方形ABCD边CD上一点，连接AF，将△ADF绕点A顺时针旋转90°与△ABG重合（D与B重合，F与G重合，此时点G，B，C在一条直线上），∠GAF的平分线交BC于点E，连接EF，判断线段EF与GE之间有怎样的数量关系，并说明理由．
（2）知识迁移
如图2，在四边形ABCD中，∠ADC+∠B=180°，AB=AD，E，F分别是边BC，CD延长线上的点，连接AE，AF，且∠BAD=2∠EAF，试写出线段BE，EF，DF之间的数量关系，并说明理由．
（3）实践创新
如图3，在四边形ABCD中，∠ABC=90°，AC平分∠DAB，点E在AB上，连接DE，CE，且∠DAB=∠DCE=60°，若DE=a,AD=b,AE=c,求BE的长．（用含a,b,c的式子表示）
发布：2025/6/14 19:0:1组卷：1975引用：4难度：0.2
