下列判断：①有两个内角分别为50°和20°的三角形一定是钝角三角形；②直角三角形中两锐角之和为90°；③三角形的三个内角中不可以有三个锐角④有一个外角是锐角的三角形一是钝角三角形，其中正确的有（ ）
【答案】C
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：165引用：3难度：0.9
相似题
-
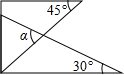1．如图是一副三角板叠放的示意图，则∠α=．发布：2025/6/19 13:0:6组卷：2455引用：64难度：0.5 -
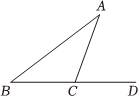2．如图，在△ABC中，∠A=30°，∠B=50°，延长BC到D，则∠ACD=°．发布：2025/6/19 13:30:1组卷：638引用：62难度：0.7 -
3．探索三角形的内（外）角平分线形成的角的规律
在三角形中，由三角形的内角平分线、外角平分线所形成的角存在一定的规律．
规律1：三角形的两个内角的平分线形成的钝角等于90°加上第三个内角度数的一半．
规律2：三角形的两个外角的平分线形成的锐角等于90°减去与这两个外角不相邻的内角度数的一半．
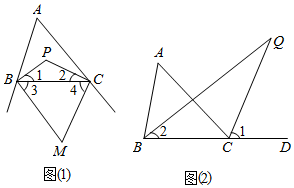
如图（1），已知点P是△ABC的内角平分线BP与CP的交点，点M是△ABC的外角平分线BM与CM的交点，则∠P=90°+∠A，∠M=90°-12∠A12
证明规律1：
∵BP、CP是△ABC的角平分线，
∴∠1=∠ABC，∠2=12∠ACB，（1）12
∴∠A=180°-2（∠1+∠2），（2）
∴∠1+∠2=90°-∠A，12
∴∠P=180°-（∠1+∠2）=90°+∠A．12
证明规律2：
∵∠3=（∠A+∠ACB），∠4=12（∠A+∠ABC），12
∴∠3+∠4=（∠A+∠ACB+∠ABC）+12∠A=90°+12∠A，12
∴∠M=180°-（∠3+∠4）=90°-∠A．12
请解决以下问题：
（1）写出上述证明过程中步骤（2）的依据是：；
（2）如图（2），已知点Q是△ABC的内角平分线BQ与△ABC的外角（∠ACD）平分线CQ的交点，请猜想∠Q和∠A的数量关系，并说明理由．发布：2025/6/19 23:30:1组卷：572引用：2难度：0.7
