观察算式：
11×2=1-12=12，
11×2+12×3=1-12+12-13=23，
11×2+12×3+13×4=1-12+12-13+13-14=34；
…
（1）按规律填空：
①11×2+12×3+13×4+14×5=4545；
②11×2+12×3+13×4+14×5+…+199×100=9910099100；
③如果n为正整数，那么11×2+12×3+13×4+14×5+…+1n×（n+1）=nn+1nn+1；
（2）计算（由此拓展写出具体过程）：
①11×3+13×5+15×7+…+199×101；
②1-12-16-112-…-19900．
1
1
×
2
=
1
1
2
=
1
2
1
1
×
2
+
1
2
×
3
=
1
1
2
+
1
2
1
3
=
2
3
1
1
×
2
+
1
2
×
3
+
1
3
×
4
=
1
1
2
+
1
2
1
3
+
1
3
1
4
=
3
4
1
1
×
2
+
1
2
×
3
+
1
3
×
4
+
1
4
×
5
4
5
4
5
1
1
×
2
+
1
2
×
3
+
1
3
×
4
+
1
4
×
5
+
…
+
1
99
×
100
99
100
99
100
1
1
×
2
+
1
2
×
3
+
1
3
×
4
+
1
4
×
5
+
…
+
1
n
×
（
n
+
1
）
n
n
+
1
n
n
+
1
1
1
×
3
+
1
3
×
5
+
1
5
×
7
+
…
+
1
99
×
101
1
2
1
6
1
12
1
9900
【考点】有理数的混合运算．
【答案】；；
4
5
99
100
n
n
+
1
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/4 1:0:8组卷：2378引用：6难度：0.1
相似题
-
1．对于有理数a、b,规定运算“*”如下：a*b=a×b-a-b-2
（1）计算：（-3）*2的值
（2）求（-2）*4*（-1）的值．发布：2025/6/15 13:30:2组卷：212引用：3难度：0.3 -
2．已知a、b皆为正有理数，定义运算符号为※：当a＞b时，a※b=2a；当a＜b时，a※b=2b-a,则3※2-（-2※3）等于（ ）
发布：2025/6/15 14:0:2组卷：468引用：6难度：0.6 -
3．日常生活中，我们使用的是十进制数，而计算机使用的数是二进制数（数位的进位方法是“逢二进一”），有时候也会用到三进制数（数位的进位方法是“逢三进一”）．如三进位制数201可用十进制数表示为2×32+0×3+1=19；二进位制数1011可用十进制数表示为1×23+0×22+1×2+1=11．
（1）现有三进位制数a=221，二进位制数b=10111，试比较a与b的大小关系．
（2）填空：将十进制数18用二进制数表示为 ．
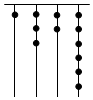
（3）我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”．如图是一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数．求孩子出生的天数．发布：2025/6/15 11:0:2组卷：287引用：1难度：0.5
