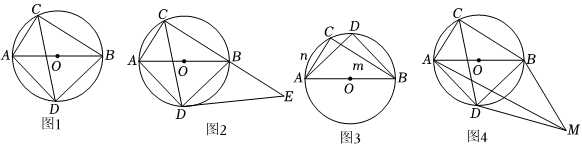
问题背景：如图1，AB是⊙O的直径，点C，点D在圆上（在直径AB的异侧），且D为弧AB的中点，连接AD，BD，CD，AC，BC．探究思路：如图2，将△ADC绕点D顺时针旋转90°得到△BDE，证明C，B，E三点共线，从而得到△DCE为等腰直角三角形，BC+BE=2CD，从而得出AC+BC=2CD．
（1）请你根据探究思路，写出完整的推理过程；
问题解决：（2）若点C，点D在直径AB的同侧，如图3所示，且点D为弧AB的中点，连接CD，BC=m,AC=n（m＞n），直接写出线段CD的长为 2（m-n）22（m-n）2（用含有m,n的式子表示）；
拓展探究：（3）将△CBD沿BD翻折得到△MBD，如图4所示，试探究：MA，MB，MD之间的数量关系，并
说明理由．
BC
+
BE
=
2
CD
AC
+
BC
=
2
CD
2
（
m
-
n
）
2
2
（
m
-
n
）
2
【考点】圆的综合题．
【答案】
2
（
m
-
n
）
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/30 8:0:9组卷：173引用：1难度：0.1
相似题
-
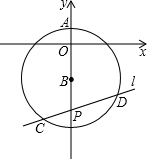1．如图，圆心B在y轴的负半轴上，半径为5的⊙B与y轴的正半轴交于点A（0，1）．过点P（0，-7）的直线l与⊙B相交于C、D两点，则弦CD长的所有可能的整数值有个；它们是．发布：2025/6/18 10:30:1组卷：365引用：2难度：0.7 -
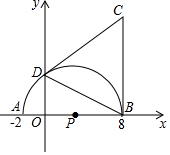2．如图，平面直角坐标系中，A（-2，0），B（8，0），以AB为直径作半圆P交y轴于点D，过点B作BC⊥x轴，且BC=10，连接CD．
（1）图中⊙P的半径长为，点D的坐标为；
（2）求证：直线CD是⊙P的切线；
（3）求tan∠CDB的值．发布：2025/6/18 13:0:8组卷：103引用：1难度：0.5 -
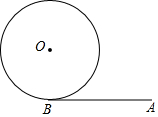3．如图，已知⊙O的半径为3，A是⊙O外一点，AB切⊙O于点B，且AB=6．
（1）求点A到⊙O上的点之间的最短距离；
（2）作AB的中垂线CD交AB于C，试判断CD与⊙O的位置关系，并证明；
（3）若⊙O上点M能与AB构成等腰三角形，请直接写出所有符合条件的BM的值．发布：2025/6/18 13:0:8组卷：256引用：1难度：0.1
