综合与实践
【问题背景】通过对同一面积的不同表达和比较来理解整式乘法公式是常见的办法，如图1，边长为（a+b）的大正方形可分割成两个较小的正方形和两个大小相同的长方形（如图2），且在图1到图2的分割过程中，面积没有变化，由此解决下列问题．
【探索归纳】
（1）若将图1中的大正方形看作一个整体，则它的面积是 （a+b）2（a+b）2（用含a,b的式子表示）；
（2）图2中4个部分的面积之和是 a2+2ab+b2a2+2ab+b2（用含a,b的式子表示）；
（3）因此，可以得到等式：（a+b）2=a2+2ab+b2（a+b）2=a2+2ab+b2．
【学以致用】简便计算：
（4）3.142+6.28×6.86+6.862．
【拓展应用】
（5）若图2中的长方形的长（b）与宽（a）的值分别为：a=12-m,b=m-3，且满足（12-m）（m-3）=18，请求出（12-m）2+（m-3）2的值．
【考点】完全平方公式的几何背景；多项式乘多项式．
【答案】（a+b）2；a2+2ab+b2；（a+b）2=a2+2ab+b2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/29 8:0:10组卷：192引用：3难度：0.5
相似题
-
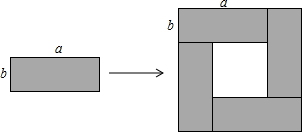1．如图将4个长、宽分别均为a,b的长方形，摆成了一个大的正方形，利用面积的不同表示方法写出一个代数恒等式是（ ）发布：2025/6/18 16:30:1组卷：5247引用：39难度：0.7 -
2．有3张边长为a的正方形纸片，4张边长分别为a、b（b＞a）的矩形纸片，5张边长为b的正方形纸片，从其中取出若干张纸片，每种纸片至少取一张，把取出的这些纸片拼成一个正方形（按原纸张进行无空隙、无重叠拼接），则拼成的正方形的边长最长可以为（ ）
发布：2025/6/19 11:30:1组卷：3332引用：74难度：0.9 -
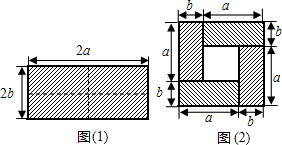
3．如图（1），是一个长为2a宽为2b（a＞b）的矩形，用剪刀沿矩形的两条对角轴剪开，把它分成四个全等的小矩形，然后按图（2）拼成一个新的正方形，求中间空白部分的面积（用含a、b的式子表示）
发布：2025/6/18 10:0:1组卷：298引用：1难度：0.5
