某公司为宣传其产品，设计一大型广告立牌置于公司楼下显目位置，广告立牌垂直于地面，其设计图如下所示，由直角△ABC和以BC为直径的半圆拼接而成，AC⊥BC，AB固定于地面，且AB=10m,点P为半圆上一点（异于B，C两点），四边形ABPC为梯形，CP∥AB，该广告立牌右侧有一条垂直于AB的直线小道L（直线小道路面与地面平齐），与AB的延长线交于点D，且BD=10m.
（1）若沿该造型外部边缘增加铁丝加以固定，求铁丝长度（即CA+ˆCPB）的最大值及此时tan∠CAB的值；
（2）若∠CAB=60°，行人M（视为质点，行人高度忽略不计）沿直线小道L向该广告立牌走近，当对底边AB观察的视线所张的角最大时，求从M处观察P点时仰角的正切值．
ˆ
CPB
【考点】解三角形．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/7 0:0:1组卷：71引用：4难度：0.5
相似题
-
1．已知灯塔A在海洋观察站C的北偏东65°，距离海洋观察站C的距离为akm,灯塔B在海洋观察站C的南偏东55°，距离海洋观察站C的距离为3akm,则灯塔A与灯塔B的距离为（ ）
发布：2024/12/30 4:0:3组卷：50引用：3难度：0.7 -
2．在①
，②2a-c=2bcosC，③（a-b）（a+b）=（a-c）c这三个条件中任选一个，补充在下面的问题中，并解答该问题．3（a-bcosC）=csinB
在△ABC中，内角A，B，C的对边分别是a,b,c,且满足 _____，．b=23
（1）若a+c=4，求△ABC的面积；
（2）求△ABC周长l的取值范围．发布：2024/12/29 13:0:1组卷：289引用：4难度：0.5 -
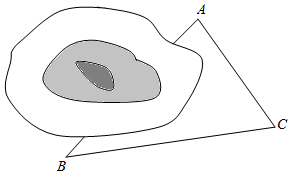3．如图，在铁路建设中，需要确定隧道两端的距离（单位：百米），已测得隧道两端点A，B到某一点C的距离分别为5和8，∠ACB=60°，则A，B之间的距离为（ ）发布：2024/12/29 13:0:1组卷：295引用：5难度：0.7
