【探究】如图①，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成图②的长方形．
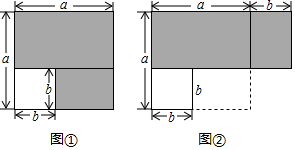
（1）请你分别表示出这两个图形中阴影部分的面积 a2-b2a2-b2； （a+b）（a-b）（a+b）（a-b）；
（2）比较两图的阴影部分面积，可以得到乘法公式：a2-b2=（a+b）（a-b）a2-b2=（a+b）（a-b）（用字母表示）；
【应用】请应用这个公式完成下列各题：
计算：（2a+b-c）（2a-b+c）．
【拓展】
①（2+1）（22+1）（24+1）（28+1）…（232+1）+1结果的个位数字为 66；
②计算：2002-1992+1982-1972+…+42-32+22-12．
【答案】a2-b2；（a+b）（a-b）；a2-b2=（a+b）（a-b）；6
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/17 11:0:10组卷：948引用：2难度：0.6
相似题
-
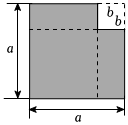1．如图，从一个边长为a的正方形的一角上剪去一个边长为b（a＞b）的正方形，则剩余（阴影）部分正好能够表示一个乘法公式，则这个乘法公式是（用含a,b的等式表示）．发布：2025/6/16 21:0:1组卷：806引用：6难度：0.7 -
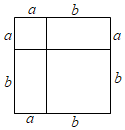2．如图，对一个正方形进行面积分割，下列等式能够正确表示该图形面积关系的是（ ）发布：2025/6/17 1:30:2组卷：346引用：2难度：0.8 -
3．数学业余小组在活动中发现：
（a-b）（a+b）=a2-b2；
（a-b）（a2+ab+b2）=a3-b3；
（a-b）（a3+a2b+ab2+b3）=a4-b4；
（a-b）（a5+a4b+a3b2+a2b3+ab4+b5）=a6-b6；
…
（a-b）（an-1+an-2b+an-3b2…+a2bn-3+abn-2+bn-1）=an-bn．；
（1）请你在答题卡中写出（补上）上述公式中积为a5-b5的一行；
（2）请仔细领悟上述公式，并将a3+b3分解因式；
（3）请将a5+a4b+a3b2+a2b3+ab4+b5分解因式．发布：2025/6/16 23:30:1组卷：430引用：2难度：0.5
