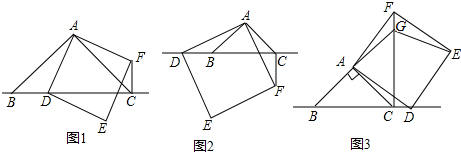
在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD的右侧作正方形ADEF，连接CF．
（1）观察猜想
如图1，当点D在线段BC上时，
①BC与CF的位置关系为：BC⊥CFBC⊥CF；
②BC，CD，CF之间的数量关系为：BC=CF+CDBC=CF+CD．（将结论直接写在横线上）
（2）数学思考
如图2，当点D在线段CB的延长线上时，结论①②是否仍然成立？若成立，请给予证明：若不成立，请你写出正确结论再给予证明，
（3）拓展延伸
如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若AB=22，CD=1，请求出GE的长．
2
【考点】四边形综合题．
【答案】BC⊥CF；BC=CF+CD
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：659引用：2难度：0.2
相似题
-
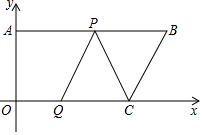1．如图，在平面直角坐标系中，AB∥OC，A（0，12），B（a,c），C（b,0），并且a,b满足b=+a-20+16．动点P从点A出发，在线段AB上以每秒2个单位长度的速度向点B运动；动点Q从点O出发，在线段OC上以每秒1个单位长度的速度向点C运动，点P，Q分别从点A，O同时出发，当点P运动到点B时，点Q随之停止运动．设运动时间为t秒．20-a
（1）直接写出B，C两点的坐标；
（2）当t为何值时，四边形PQCB是平行四边形？
（3）当t为何值时，△PQC是以PQ为腰的等腰三角形？并求出P，Q两点的坐标．发布：2025/6/5 10:0:2组卷：450引用：5难度：0.2 -
2．如图，在边长为4的正方形ABCD中，点P在AB上从A向B运动，连接DP交AC于点Q．
（1）试证明：无论点P运动到AB上何处时，都有△ADQ≌△ABQ；
（2）当△ABQ的面积是正方形ABCD面积的时，求DQ的长；16
（3）若点P从点A运动到点B，再继续在BC上运动到点C，在整个运动过程中，当点P运动到什么位置时，△ADQ恰为等腰三角形．发布：2025/6/5 10:0:2组卷：268引用：11难度：0.3 -
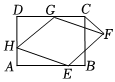3．已知，如图，矩形ABCD中，AD=6，DC=8，菱形EFGH的三个顶点E，G，H分别在矩形ABCD的边AB，CD，DA上，AH=2，连接CF．
（1）若DC=2，求证：四边形EFGH为正方形；
（2）当点G在边CD上运动时，点F到直线CD的距离是否为定值？若是，请求出这个定值；若不是，请说明理由．
（3）试说明当点C运动到何处时，△FCG的面积最小，并求出这个最小值．
发布：2025/6/5 9:30:2组卷：25引用：1难度：0.2
