在△ABC中，∠BAC=90°，AB=AC，D为BC上一点，连结AD．
（1）如图1，点D不与B、C重合，用等式表示AD、BD、CD之间的数量关系，并证明；
（2）如图2，延长CB至E使得BE=BD，若∠BAD=7.5°，用等式表示AD与AE的数量关系，并证明．
【考点】三角形综合题．
【答案】（1）2AD2=BD2+CD2，证明见解析；
（2）．证明见解析．
（2）
（
3
-
2
）
A
D
2
=
A
E
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/26 8:0:9组卷：77引用：1难度：0.5
相似题
-
1．已知：等边△ABC中．
（1）如图1，点M是BC的中点，点N在AB边上，满足∠AMN=60°，求的值；ANBN
（2）如图2，点M在AB边上（M为非中点，不与A、B重合），点N在CB的延长线上且∠MNB=∠MCB，求证：AM=BN．
（3）如图3，点P为AC边的中点，点E在AB的延长线上，点F在BC的延长线上，满足∠AEP=∠PFC，求的值．BF-BEBC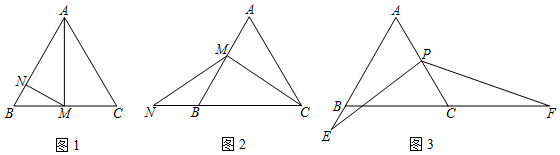
发布：2025/6/12 4:0:1组卷：1053引用：4难度：0.3 -
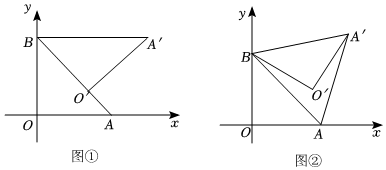2．在平面直角坐标系中，点A（2，0），点B（0，2）分别是坐标轴上的点，连接AB．把△ABO绕点B逆时针旋转得△A′BO′．点A，O旋转后的对应点为点A′，O′．记旋转角为α．
（Ⅰ）如图①，当点O′落在AB边上时，求α的值和点O′的坐标：
（Ⅱ）如图②，当α=60°时，求AA′的长和点O′的坐标：
（Ⅲ）连接AO′，直接写出在旋转过程中△AO′A′面积的最大值．发布：2025/6/12 4:30:1组卷：1018引用：7难度：0.1 -
3．如图①，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重叠部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重叠部分；…将余下部分沿∠BnAnC（n为正整数）的平分线AnBn+1折叠，点与点C重合．无论折叠多少次，只要最后一次Bn与点恰好重合，我们就称∠ABC是△ABC的好角．
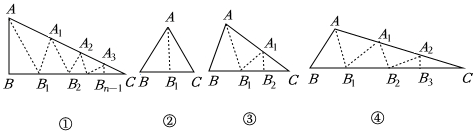
小丽展示了确定∠BAC是△ABC的好角的两种情形．
情形一：如图②，沿等腰三角形ABC顶角∠BAC是平分线AB1折叠，点B与点重合；
情形二：如图③，沿△ABC的∠BAC的平分线AB1折叠，剪掉重叠部分；将余下的部分沿∠B1A1C的平分线A1B2折叠，此时点B1与点C重合．
【探究发现】
（1）如图③，△ABC中，∠B=2∠C，经过两次折叠，∠BAC是不是△ABC的好角？．（填：“是”或“不是”）
（2）归纳猜想：
①如图④，小丽经过三次折叠发现了∠BAC是△ABC的好角，请探究∠B与∠C（∠B＞∠C）之间的等量关系，并说明理由．
②根据以上内容猜想：若经过n（n为正整数）次折叠∠BAC是好角，则∠B与∠C（∠B＞∠C）之间的等量关系为 ．（直接写出结论）
【应用提升】
（3）小丽找到一个三角形，三个角分别为15°，60°，105°，发现60°和105°的两个角都是此三角形的好角，如果一个三角形的最小角是18°，请直接写出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．发布：2025/6/12 6:0:2组卷：75引用：1难度：0.2
