数学家波利亚说过:“为了得到一个方程,我们必须把同一个量用两种不同的方法表示出来,即将一个量算两次,从而建立等量关系.”这就是“算两次”原理,也称为富比尼(G.Fubini)原理.例如:对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.计算图1的面积,把图1看作一个大正方形,它的面积是(a+b)2;如果把图1看作是由2个长方形和2个小正方形组成的,它的面积为a2+2ab+b2.由此得到(a+b)2=a2+2ab+b2.
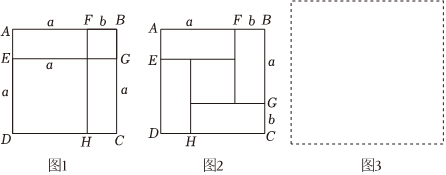
(1)如图2,正方形ABCD是由四个边长为a,b的全等的长方形和中间一个小正方形组成的,用不同的方法对图2的面积进行计算,你发现的等式是 (a+b)2=(a-b)2+4ab(a+b)2=(a-b)2+4ab(用a,b表示);
(2)请你用若干块如图1所示的长方形和正方形硬纸片图形,用拼长方形的方法,把下列二次三项式进行因式分解:a2+3ab+2b2.要求:在图3的框中画出图形,写出分解的因式;
(3)请你用(1)发现的等式解决问题:已知两数x,y满足x+y=3,xy=54,求x2-y2的值.
xy
=
5
4
【考点】因式分解的应用;完全平方公式的几何背景.
【答案】(a+b)2=(a-b)2+4ab
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/18 7:0:2组卷:173引用:4难度:0.5
相似题
-
1.若正整数x、y满足x2-y2=2019,则这样的数对(x,y)个数是( )
发布:2025/6/12 16:30:2组卷:135引用:2难度:0.6 -
2.对于任意一个四位数N,如果N满足各个数位上的数字互不相同.且个位数字不为0,N的百位数字与十位数字之差是千位数字与个位数字之差的2倍,则称这个四位数N为“双减数”,对于一个“双减数”N=
,将它的千位和百位构成的两位数为abcd,个位和十位构成的两位数为ab,规定:F(N)=dc.ab-dc12
例如:N=7028.因为0-2=2×(7-8),所以7028是一个“双减数”则F(7028)==-1.70-8212
(1)判断3401,5713是否是“双减数”,并说明理由;如果是,求出F(N)的值;
(2)若“双减数”M的各个数位上的数字之和能被11整除,且F(M)是3的倍数,求M的值.发布:2025/6/12 16:0:1组卷:279引用:3难度:0.4 -
3.对一个任意三位数M=a
c,如果M满足各个数位上的数字互不相同,且都不为零,现将M各个数位上的数字从左往右由大到小排列得到一个新数M1,将M各个数位上的数字从左往右由小到大排列得到一个新数M2,记F(M)=b,如果F(M)为整数,则称M为“7倍和数”.M1+M27
例如:M=326,则F(326)==124是整数,所以326是“7倍和数”;M=123,则F(123)=632+2367=63321+1237不是整数,所以123不是“7倍和数”.37
(1)判断324,745是否是“7倍和数”,并说明理由;
(2)T=100a+90+b(1≤a<b<9),a,b都是正整数,T是“7倍和数”,求T的值.发布:2025/6/12 16:0:1组卷:43引用:1难度:0.5


