著名的赵爽弦图（如图①，其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c），大正方形的面积可以表示为c2，也可以表示为4×12ab+（a-b）2，由此推导出直角三角形的三边关系：如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2．
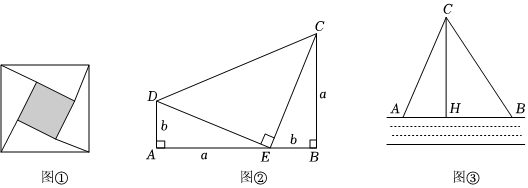
（1）图②为美国第二十任总统伽菲尔德的“总统证法”，请你利用图②推导上面的关系式．利用以上所得的直角三角形的三边关系进行解答：
（2）如图③，在一条东西走向河流的一侧有一村庄C，河边原有两个取水点A，B，其中AB=AC，由于某种原因，由C到A的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点H（A、H、B条直线上），并新修一条路CH，且CH⊥AB．测得CH=6千米，HB=4.5千米，求新路CH比原路CA少多少千米？
（3）在第（2）问中若AB≠AC时，CH⊥AB，AC=8，BC=10，AB=12，设AH=x,求x的值．
4
×
1
2
ab
+
（
a
-
b
）
2
【考点】勾股定理的证明．
【答案】（1）见详解；
（2）0.25；
（3）x=．
（2）0.25；
（3）x=
9
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/8 2:0:2组卷：244引用：2难度：0.5
相似题
-
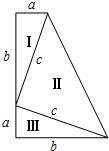1．如图，三个直角三角形（Ⅰ，Ⅱ，Ⅲ）拼成一个直角梯形（两底分别为a、b,高为a+b），利用这个图形，小明验证了勾股定理．请你填写计算过程中留下的空格：
S梯形=（上底+下底）•高=12（a+b）•（a+b），即S梯形=12（）①12
S梯形=Ⅰ+Ⅱ+Ⅲ（罗马数字表示相应图形的面积）
=++，即S梯形=（）②12
由①、②，得a2+b2=c2．发布：2025/6/17 20:30:2组卷：305引用：2难度：0.7 -
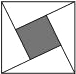2．“赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形．如图，每一个直角三角形的两条直角边的长分别是3和6，则中间小正方形与大正方形的面积差是（ ）发布：2025/6/17 19:30:1组卷：3427引用：3难度：0.5 -
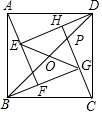3．如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH．连接EG，BD相交于点O，BD与HC相交于点P．若GO=GP，则的值是（ ）S正方形ABCDS正方形EFGH发布：2025/6/17 22:0:1组卷：5295引用：33难度：0.6
