综合与探究
（1）如图1，AO∥CP，OB∥PD，则∠AOB与∠CPD之间的数量关系为 ∠AOB=∠CPD∠AOB=∠CPD；如图2，AO∥CP，OB∥PD，则∠AOB与∠CPD之间的数量关系为 ∠AOB+∠CPD=180°∠AOB+∠CPD=180°；
（2）在图3中，AB∥CD，AF∥CE，EF∥CD，∠A=45°，求∠E的度数．
（3）在图4中，AD∥CF，DE∥BC，AB∥FG，AD平分∠EDH，试探究∠ABC、∠DHF与∠CFG之间的数量关系．
【考点】平行线的判定与性质．
【答案】∠AOB=∠CPD；∠AOB+∠CPD=180°
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/2 8:0:9组卷：105引用：1难度：0.5
相似题
-
1．几何说理填空：如图，F是BC上一点，FG⊥AC于点G，H是AB上一点，HE⊥AC于点E，∠1=∠2，求证：DE∥BC．
证明：连接EF
∵FG⊥AC，HE⊥AC，
∴∠FGC=∠HEC=90°（ ）．
∴∥（ ）．
∴∠3=∠（ ）．
又∵∠1=∠2，
∴∠1+∠3=∠2+∠4．
即∠DEF=∠EFC
∴DE∥BC（ ）．发布：2025/6/8 3:30:1组卷：1052引用：10难度：0.7 -
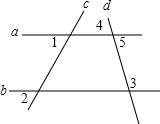2．已知：如图，∠1=∠2．求证：∠3+∠4=180°
证明：∵∠1=∠2
∴a∥b （）
∴∠3+∠5=180° （）
又∵∠4=∠5（）
∴∠3+∠4=180°发布：2025/6/8 3:30:1组卷：158引用：2难度：0.8 -
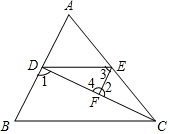3．完成下面的证明：
如图，已知∠1、∠2互为补角，且∠3=∠B，
求证：∠AED=∠ACB．
证明：∵∠1+∠2=180°，∠2+∠4=180°
∴∠1=∠4 （）
∴AB∥EF（）
∴∠3=（）
又∠3=∠B
∴∠B=（）
∴DE∥BC （）
∴∠AED=∠ACB （）发布：2025/6/8 4:0:1组卷：766引用：9难度：0.6
