过点P用两种不同的方法，利用直尺和圆规作直线l,交∠MAN两边于B、C，使得△ABC为等腰三角形．（保留作图痕迹，不写作法）
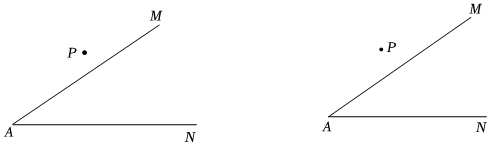
【考点】作图—复杂作图．
【答案】见解析．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/16 11:0:2组卷：616引用：1难度：0.5
相似题
-
1．如图，在数轴上，三个有理数从左到右依次是：-1，x,x+1．
（1）利用刻度尺或圆规，在数轴上画出原点；
（2）记长为2个单位，宽为1个单位的长方形的对角线长为a,请在数轴上画出表示a的点．
发布：2025/6/13 8:30:1组卷：107引用：2难度：0.5 -
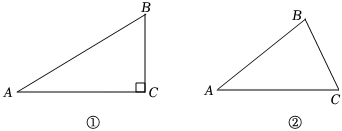2．利用圆规和无刻度的直尺，求作：⊙O，使圆心O位于线段AC上，⊙O过点C且与AB相切．
（1）如图①，已知Rt△ABC中，∠C=90°；
（2）如图②，已知△ABC，∠C≠90°．发布：2025/6/13 5:0:1组卷：268引用：3难度：0.4 -
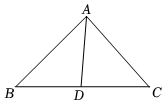3．如图，在△ABC中，点D为BC边上的中点，连接AD．
（1）尺规作图：在BC下方作射线BF，使得∠CBF=∠C，且射线BF交AD的延长线于点E（不要求写作法，保留作图痕迹）；
（2）在（1）所作的图中，连接CE，若CE=AC，求证：四边形ABEC是菱形．（请补全下面的证明过程）
证明：∵点D为BC边上的中点，
∴DC=DB，在△ADC和△EDB中，∠ACD=∠EBDDC=DB∠ADC=∠EDB
∴△ADC≌（ASA），
∴AC=，
∵∠CBF=∠ACB，
∴AC∥．
∴四边形ABEC是平行四边形．
又∵，
∴平行四边形ABEC是菱形．发布：2025/6/13 7:30:2组卷：200引用：9难度：0.5
