甲、乙两人共同设计了一条从A地到B地,B地到C地,C地到D地的路线.某一天上午10点,甲骑自行车从A地出发,沿该路线匀速行驶40千米后恰好到达B地,到达B地的时间是当天中午12点,在B地原地休息30分钟后,以原来的速度沿该路线匀速行驶40千米后恰好到达C地,到达C地后立即以原来的速度按原行驶路线匀速行驶返回A地.在甲出发x小时后,乙开小汽车从A地出发,沿该路线匀速行驶直接到达C地,到达C地后立即沿该路线匀速行驶5千米恰好到达D地,在D地休息y小时后,立即以原来的速度按原行驶路线匀速行驶返回A地.已知在行驶的过程中,乙的速度是甲的3倍.
(1)求甲、乙两人行驶的速度;
(2)在甲从B地到C地的行驶过程中,若乙与甲第一次相遇,且相遇地点不与B地和C地重合,求x的取值范围;
(3)当x=3时,甲、乙两人能否在B地与C地之间(不包括B地与C地)相遇2次?如果能,请求出y的取值范围,如果不能,请说明理由.
【考点】一元一次方程的应用.
【答案】(1)20;60;(2)<x<;(3)当0<y<时,甲、乙两人能在B地与C地之间相遇2次.
11
6
19
6
7
12
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/8 8:0:9组卷:87引用:1难度:0.7
相似题
-
1.如图,一个点从数轴上的原点开始,先向左移动1cm到达A点,再向左移动3cm到达B点,然后向右移动9cm到达C点.
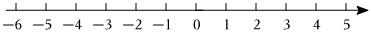
(1)用1个单位长度表示1cm,请你在数轴上表示出A,B,C三点的位置;
(2)把点C到点A的距离记为CA,求CA的长度?
(3)若点B以每秒2cm的速度向左移动,同时A、C点分别以每秒1cm、4cm的速度向右移动,设移动时间为t秒,试探索:CA-AB的值是否会随着t的变化而改变?请说明理由.发布:2025/6/9 0:30:2组卷:71引用:1难度:0.6 -
2.5月份,甲、乙两个工厂用水量共为200吨.进入夏季用水高峰期后,两工厂积极响应国家号召,采取节水措施,6月份,甲工厂用水量比5月份减少了15%,乙工厂用水量比5月份减少了10%,两个工厂6月份用水量共为174吨,求两个工厂6月份的用水量各是多少吨.
发布:2025/6/8 23:0:1组卷:140引用:1难度:0.6 -
3.如图,数轴上A、B、C三点对应的有理数分别为10、15和-5.若点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.

(1)探究:
①AB的长度为 个单位长;AC的长度为 个单位长.
②若数轴上有M、N两点,对应的有理数为x、y,且y>x,则MN的长度为 个单位长(用x、y的式子表示).
(2)应用:
①当0<t<5时,用含t的式子填空:BP=个单位长,AQ=个单位长;
②当t=2时,求PQ的值;
(3)拓展:
当P、Q两点距离为4个单位长度时,求t的值.发布:2025/6/9 0:0:2组卷:450引用:2难度:0.5


