某高校男、女学生人数基本相当,为了解该校英语四级考试情况,随机抽取了该校首次参加英语四级考试的男、女各60名学生的成绩,情况如表:
| 合格 | 不合格 | |
| 男生 | 35 | 25 |
| 女生 | 45 | 15 |
(2)从这60名男生中任意选2人,求这2人中合格人数的概率分布及数学期望;
(3)将抽取的这120名学生合格的频率视为该校首次参加英语四级考试的每位学生合格的概率.若学生首次考试不合格,则经过一段时间的努力,第二次参加考试合格的概率会增加
1
6
附:
K
2
=
n
(
ad
-
bc
)
2
(
a
+
b
)
(
c
+
d
)
(
a
+
c
)
(
b
+
d
)
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
【考点】离散型随机变量的均值(数学期望).
【答案】(1)没有99%的把握认为该校首次参加英语四级考试的学生能否合格与性别有关;
(2)分布列见解析,数学期望为;
(3)概率为.
(2)分布列见解析,数学期望为
7
6
(3)概率为
289
324
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/26 15:0:2组卷:54引用:4难度:0.5
相似题
-
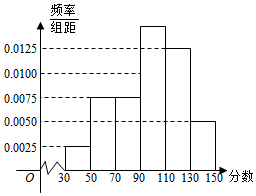 1.某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间(30,150]内,其频率分布直方图如图.
1.某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间(30,150]内,其频率分布直方图如图.
(Ⅰ)求获得复赛资格的人数;
(Ⅱ)从初赛得分在区间(110,150]的参赛者中,利用分层抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间(110,130]与(130,150]各抽取多少人?
(Ⅲ)从(Ⅱ)抽取的7人中,选出3人参加全市座谈交流,设X表示得分在区间(130,150]中参加全市座谈交流的人数,求X的分布列及数学期望E(X).发布:2024/12/29 13:30:1组卷:134引用:7难度:0.5 -
2.设离散型随机变量X的分布列如表:
若离散型随机变量Y=-3X+1,且E(X)=3,则( )X 1 2 3 4 5 P m 0.1 0.2 n 0.3 发布:2024/12/29 13:0:1组卷:199引用:6难度:0.5 -
3.从4名男生和2名女生中任选3人参加演讲比赛,用X表示所选3人中女生的人数,则E(X)为( )
发布:2024/12/29 13:30:1组卷:139引用:6难度:0.7


