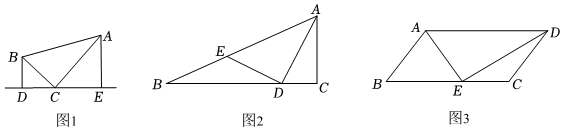
(1)如图1,在△ABC中,∠ACB=90°,直线l过点C,分别过A、B两点作AE⊥l,BD⊥l,垂足分别为E、D.求证:△BDC∽△CEA;
(2)如图2,在△ABC中,∠ACB=90°,D是BC上一点,连接AD,过D作AD的垂线交AB于点E.若BE=DE,DEDA=45,AC=20,求BD的长;
(3)如图3,平行四边形ABCD是一个农博园的一块空地示意图,农博园设计部门计划将该空地设计成由两种花卉构成的花园,点E在边BC上,在△ADE区域种植郁金香,造价每平方米180元,在其他区域种植孔雀草,造价每平方米100元,根据造型设计要求,∠AED=90°,AE=AB,BEEC=43,CD=1014米,试求完成这两种鲜花的种植需要的费用为多少元?(结果保留根号)
DE
DA
=
4
5
BE
EC
=
4
3
CD
=
10
14
【考点】相似形综合题.
【答案】(1)证明见解析过程;
(2)32;
(3)元.
(2)32;
(3)
98000
10
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/6 8:0:9组卷:135引用:3难度:0.5
相似题
-
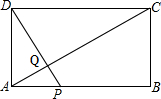 1.如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
1.如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.
①当t为何值时,DP⊥AC?
②设S△APQ+S△DCQ=y,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.发布:2025/7/1 13:0:6组卷:2098引用:6难度:0.1 -
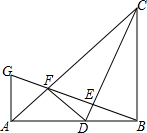 2.如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连接CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF,给出以下四个结论:①=AGAB;②若点D是AB的中点,则AF=AFFCAB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若23=DBAD,则S△ABC=9S△BDF,其中正确的结论序号是( )12发布:2025/6/24 16:30:1组卷:2783引用:11难度:0.2
2.如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连接CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF,给出以下四个结论:①=AGAB;②若点D是AB的中点,则AF=AFFCAB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若23=DBAD,则S△ABC=9S△BDF,其中正确的结论序号是( )12发布:2025/6/24 16:30:1组卷:2783引用:11难度:0.2 -
3.【探究发现】如图1,△ABC是等边三角形,∠AEF=60°,EF交等边三角形外角平分线CF所在的直线于点F,当点E是BC的中点时,有AE=EF成立;
【数学思考】某数学兴趣小组在探究AE、EF的关系时,运用“从特殊到一般”的数学思想,通过验证得出如下结论:
当点E是直线BC上(B,C除外)任意一点时(其它条件不变),结论AE=EF仍然成立.
假如你是该兴趣小组中的一员,请你从“点E是线段BC上的任意一点”;“点E是线段BC延长线上的任意一点”;“点E是线段BC反向延长线上的任意一点”三种情况中,任选一种情况,在备用图1中画出图形,并证明AE=EF.
【拓展应用】当点E在线段BC的延长线上时,若CE=BC,在备用图2中画出图形,并运用上述结论求出S△ABC:S△AEF的值.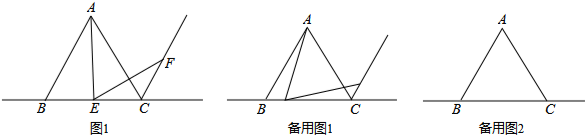 发布:2025/6/24 15:30:2组卷:1873引用:6难度:0.1
发布:2025/6/24 15:30:2组卷:1873引用:6难度:0.1


