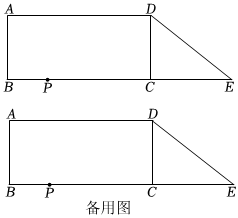
如图，在四边形ABCD中，∠A=∠B=∠BCD=90°，AB=DC=3，AD=BC=7．延长BC到E，使CE=4，连接DE，由直角三角形的性质可知DE=5．动点P从点B出发，以每秒2个单位的速度沿BC-CD-DA向终点A运动，设点P运动的时间为t秒．（t＞0）．
（1）当t=3时，BP=66；
（2）当4＜t＜5时，CP=2t-72t-7；（用含t的代数式表示）
（3）当t=77时，点P运动到∠B的角平分线上；
（4）请用含t的代数式表示△ABP的面积S；（不包括点P与点A，点B重合的情况）
（5）当点P在BC边上时，直接写出点P到四边形ABED任意相邻两边距离相等时t的值．
【考点】四边形综合题．
【答案】6；2t-7；7
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/15 8:0:9组卷：63引用：1难度：0.1
相似题
-
1．（1）证明推断：如图（1），在正方形ABCD中，点E，Q分别在边BC，AB上，DQ⊥AE于点O，点G，F分别在边CD，AB上，GF⊥AE．求证：AE=FG；
（2）类比探究：如图（2），在矩形ABCD中，=k（k为常数）．将矩形ABCD沿GF折叠，使点A落在BC边上的点E处，得到四边形FEPG，EP交CD于点H，连接AE交GF于点O．试探究GF与AE之间的数量关系，并说明理由；BCAB
（3）拓展应用：在（2）的条件下，连接CP，当时k=，若tan∠CGP=34，GF=243，求CP的长．5
发布：2025/5/24 10:30:2组卷：3153引用：13难度：0.4 -
2．综合与实践
数学活动：
数学活动课上，老师提出如下数学问题：
已知四边形ABCD与四边形BEFG都为正方形，P为DF的中点，连接AP，EP，如图1，当点E在AB上时，求证：AP=PE．
独立思考
（1）请你证明老师提出的问题；
合作交流
（2）解决完上述问题后，“翱翔”小组的同学受此启发，把正方形BEFG绕点B顺时针旋转，当点F落在对角线BD上时（如图2），他们认为老师提出的结论仍然成立．请你予以证明；
问题解决
（3）解决完上述问题后，“善思”小组提出如下问题，把正方形BEFG绕点B顺时针旋转（如图3），当点D，E，F在同一条直线上时，DE与BC交于点H．若AD=2，BG=2，请直接写出HC的值．2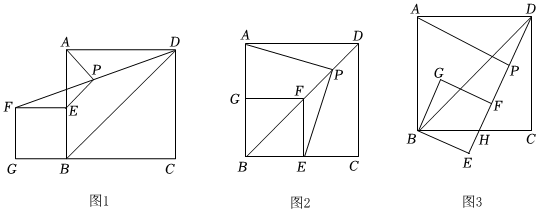
发布：2025/5/24 10:0:2组卷：621引用：1难度：0.4 -
3．数学学习总是循序渐进、不断延伸拓展的，数学知识往往起源于人们为了解决某些问题，通过观察、测量、思考、猜想出的一些结论．但是所猜想的结论不一定都是正确的．人们从已有的知识出发，经过推理、论证后，如果所猜想的结论在逻辑上没有矛盾，就可以作为新的推理的前提，数学中称之为定理．
（1）推理证明：
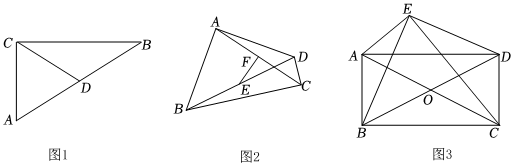
在八年级学习等腰三角形和直角三角形时，借助工具测量就能够发现：“直角三角形斜边上的中线等于斜边的一半”，当时并未说明这个结论的正确性．九年级学习了矩形的判定和性质之后，就可以解决这个问题了．如图1，在Rt△ABC中，若CD是斜边AB上的中线，则，请你用矩形的性质证明这个结论的正确性．CD=12AB
（2）迁移运用：利用上述结论解决下列问题：
①如图2，在线段BD异侧以BD为斜边分别构造两个直角三角形△ABD与△CBD，E、F分别是BD、AC的中点，判断EF与AC的位置关系并说明理由；
②如图3，▱ABCD对角线AC、BD相交于点O，分别以AC、BD为斜边且在同侧分别构造两个直角三角形△ACE与△BDE，求证：▱ABCD是矩形．发布：2025/5/24 10:30:2组卷：291引用：3难度：0.5
