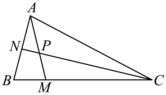
已知在△ABC中，点M是BC边上靠近点B的四等分点，点N在AB边上，且AN=NB，设AM与CN相交于点P．记AB=m，AC=n．
（1）请用m，n表示向量AM；
（2）若|n|=2|m|，设m，n的夹角为θ，若cosθ=14，求证：CN⊥AB．
AN
=
NB
AB
=
m
AC
=
n
m
n
AM
|
n
|
=
2
|
m
|
m
n
cosθ
=
1
4
CN
⊥
AB
【答案】（1）；
（2）证明见解析．
AM
=
3
4
m
+
1
4
n
（2）证明见解析．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/23 8:0:8组卷：165引用：7难度：0.7
