问题背景：如图1，某车间生产了一个竖直放在地面上的零件AB，过点A搭了一个支架AC，测得支架AC与地面成60°角，即∠ACB=60°；在AC的中点D处固定了一个激光扫描仪，需要对零件AB进行扫描，已知扫描光线的张角恒为60°，即∠EDF=60°．
问题提出：数学兴趣小组针对这个装置进行探究，研究零件AB边上的被扫描部分（即线段EF），和未扫到的部分（即线段AE和线段BF）之间的数量关系．
问题解决：
（1）先考虑特殊情况：
①如果点E刚好和点A重合，或者点B刚好和点F重合时，AE+BF ==EF（填“＞”，“＜”或“=”）；
②当点E位于特殊位置，比如当∠ADE=30°时，AE+BF ＞＞EF（填“＞”或“＜”）；
（2）特殊到一般：猜想：如图2，当0°＜∠ADE＜60°时，AE+BF 3232EF，证明你所得到的结论：
（3）研究特殊关系：如果BF2+EF2=AE2，求出EFAE的值．
3
2
3
2
EF
AE
【考点】相似形综合题．
【答案】=；＞；
3
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/26 15:0:2组卷：81引用：2难度：0.5
相似题
-
1．如图1，在△ABC中，∠BCA=90°，AC=3，BC=4，点P为斜边AB上一点，过点P作射线PD⊥PE，分别交AC、BC于点D，E．
（1）问题产生
若P为AB中点，当PD⊥AC，PE⊥BC时，=；PDPE
（2）问题延伸
在（1）的情况下，将若∠DPE绕着点P旋转到图2的位置，的值是否会发生改变？如果不变，请证明；如果改变，请说明理由；PDPE
（3）问题解决
如图3，连接DE，若△PDE与△ABC相似，求BP的值．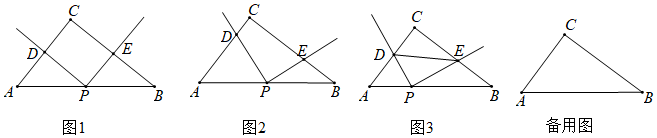
发布：2025/6/14 0:0:1组卷：966引用：6难度：0.1 -
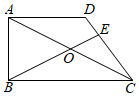2．如图，在四边形ABCD中，AD∥BC，∠ABC=90°，AD=CD，O是对角线AC的中点，联结BO并延长交边CD或边AD于点E．
（1）当点E在CD上，
①求证：△DAC∽△OBC；
②若BE⊥CD，求的值；ADBC
（2）若DE=2，OE=3，求CD的长．发布：2025/6/13 20:0:1组卷：4158引用：7难度：0.4 -
3．从三角形（不是等腰三角形）的一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中，一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．
（1）如图①，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线；
（2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数；
（3）如图②，在△ABC中，AC=3，BC=，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．3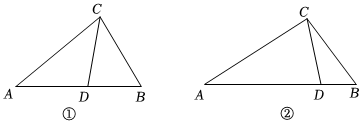
发布：2025/6/13 23:0:1组卷：439引用：2难度：0.2
