数学小组在学习“一元一次不等式与一次函数”这一节课后，尝试解决“一元一次不等式与其它函数”的关系问题．他们确定以函数y=|x+1|为研究对象，通过作图，观察图象，归纳性质等探究过程，进一步理解一元一次不等式与函数的关系．
请根据以下探究过程，回答问题．
（1）作出函数y=|x+1|的图象．
①列表：

x … -4 -3 -2 -1 0 1 2 …

y … 3 a 1 0 1 2 3 …

其中，表格中a的值为
2
2
；
②描点，连线：
根据表格的数据，请在直角坐标系中描出对应值为坐标的点，并画出该函数的图象；
（2）观察函数y=|x+1|的图象，回答下列问题：
①当x=
-1
-1
时，函数y=|x+1|有最小值，最小值为
0
0
；
②当
x＞-1
x＞-1
时（填自变量x的取值范围），y随x的增大而增大；
（3）已知直线
y
=
-
1
3
x
+
1
，请结合图象，直接写出不等式
-
1
3
x
+
1
＞
|
x
+
1
|
的解集是
-3＜x＜0
-3＜x＜0
；
（4）若直线
y
=
kx
+
1
2
与y=|x+1|有2个交点，则k的取值范围是
-1＜k＜
1
2
-1＜k＜
1
2
．

【答案】2；-1；0；x＞-1；-3＜x＜0；-1＜k＜

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/8/1 8:0:9组卷：1200引用：5难度：0.5

相似题

1．若一次函数y=kx+b的图象过点（-2，0）、（0，1），则不等式k（x-1）+b＞0的解集是（　　）
A．x＞-2 B．x＞-1 C．x＞1 D．x＞2
发布：2025/5/25 15:0:2组卷：759引用：4难度：0.6
解析
2．已知函数y=3x+1的图象经过点A（
2
3
，m），则关于x的不等式3x＜m-1的解集为（　　）
A．x＜
3
2
B．x＜
2
3
C．x＞-
3
2
D．x＞-
2
3
发布：2025/5/25 15:0:2组卷：672引用：3难度：0.6
解析

3．探究函数性质时，我们经历了列表、描点、连线画出函数图象，观察分析图象特征，概括函数性质的过程．结合已有的学习经验，请画出函数y=-
12
x
2
+
2
的图象并探究该函数的性质．

x … -4 -3 -2 -1 0 1 2 3 4 …

y … -
2
3
a -2 -4 b -4 -2 -
12
11
-
2
3
…

（1）列表，写出表中a,b的值：a=
，b=
；
描点、连线，在所给的平面直角坐标系中画出该函数的图象．
（2）观察函数图象，判断下列关于函数性质的结论是否正确（在答题卡相应位置正确的用“√”作答，错误的用“×”作答）：
①函数y=-
12
x
2
+
2
的图象关于y轴对称；
②当x=0时，函数y=-
12
x
2
+
2
有最小值，最小值为-6；
③在自变量的取值范围内函数y的值随自变量x的增大而减小．
（3）已知函数y=-
2
3
x-
10
3
的图象如图所示，结合你所画的函数图象，直接写出不等式-
1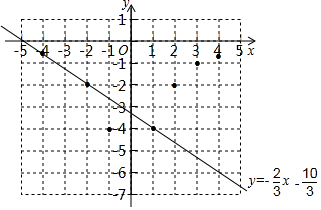2
x
2
+
2
＜-
2
3
x-
10
3
的解集．

发布：2025/5/25 16:0:2组卷：1775引用：15难度：0.6