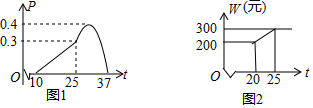某农作物的生长率p与温度t（℃）有如下关系：如图1，当10≤t≤25时可近似用函数p=150t-15刻画；当25≤t≤37时可近似用函数p=-1160（t-h）2+0.4刻画．
（1）求h的值；
（2）按照经验，该作物提前上市的天数m（天）与生长率p满足函数关系如表：
p
=
1
50
t
-
1
5
p
=
-
1
160
（
t
-
h
）
2
+
0
.
4
| 生长率p | 0.2 | 0.25 | 0.3 | 0.35 |
| 提前上市的天数m（天） | 0 | 5 | 10 | 15 |
②请用含t的代数式表示m.
（3）天气寒冷，大棚加温可改变农作物生长速度．在（2）的条件下，原计划大棚恒温20℃时，每天的成本为200元，该作物30天后上市时，根据市场调查：每提前一天上市售出（一次售完），销售额可增加800元．因此给大棚继续加温，加温后每天成本w（元）与大棚温度t（℃）之间的关系如图2．问提前上市多少天时增加的利润最大？并求这个最大利润（农作物上市售出后大棚暂停使用）．
【考点】二次函数的应用．
【答案】（1）h=29；
（2）①m=100p-20；②当10≤t≤25时，m=2t-40；当25≤t≤37时，m=-（t-29）2+20；
（3）当t=29时，提前上市20天，增加的利润最大值为19000元．
（2）①m=100p-20；②当10≤t≤25时，m=2t-40；当25≤t≤37时，m=-
5
8
（3）当t=29时，提前上市20天，增加的利润最大值为19000元．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：492引用：3难度：0.3
相似题
-
1．小明同学利用寒假30天时间贩卖草莓，了解到某品种草莓成本为10元/千克，在第x天的销售量与销售单价如下（每天内单价和销售量保持一致）：
设第x天的利润w元．销售量m（千克） m=40-x 销售单价n（元/千克） 当1≤x≤15时，n=20+ x12当16≤x≤30时，n=10+ 300x
（1）请计算第几天该品种草莓的销售单价为25元/千克？
（2）这30天中，该同学第几天获得的利润最大？最大利润是多少？注：利润=（售价-成本）×销售量
（3）在实际销售的前15天中，草莓生产基地为刺激销售，鼓励销售商批发草莓，每批发1千克就发给a（a≥2）元奖励．通过销售记录发现，前8天中，每天获得奖励后的利润随时间x（天）的增大而增大，试求a的取值范围．12发布：2025/6/18 3:0:1组卷：593引用：2难度：0.5 -
2．图2是图1中拱形大桥的示意图，桥拱与桥面的交点为O，B，以点O为原点，水平直线OB为x轴，建立平面直角坐标系，桥的拱形可近似看成抛物线y=-
（x-80）2+16，桥拱与桥墩AC的交点C恰好在水面，有AC⊥x轴，若OA=10米，则桥面离水面的高度AC为（ ）1400
发布：2025/6/18 14:0:1组卷：4971引用：62难度：0.9 -
3．心理学家发现：学生对提出概念的接受能力y与提出概念的时间x（min）之间满足二次函数关系y=-0.1x2+2.6x+43．则使学生对概念的接受能力最大．则提出概念的时间应为（ ）
发布：2025/6/18 3:30:2组卷：139引用：2难度：0.8
