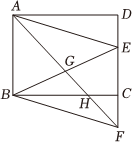
如图，在矩形ABCD中，AB=5，BC=6，点E是边CD上一动点（点E不与C、D重合），延长DC到点F，使得CF=DE，连接AF与BE交于点G，AF与BC交于点H，连接AE，BF．
（1）求证：①△ABG≌△FEG；②AE∥BF；
（2）若AG=AB，求线段GH的长；
（3）点E在运动过程中，△FEG的面积大小是否发生改变？若改变，请说明理由；若不改变，请求出△FEG的面积．
【考点】四边形综合题．
【答案】（1）证明见解答．
（2）线段GH的长为．
（3）△FEG的面积大小不变．△FEG的面积为．
（2）线段GH的长为
5
4
（3）△FEG的面积大小不变．△FEG的面积为
15
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/29 8:0:10组卷：70引用：1难度：0.3
相似题
-
1．综合与实践：
发现问题：
如图①，已知：△OAB中，OB=3，将△OAB绕点O逆时针旋转90°得△OA′B，连接BB′．
则BB′=．
问题探究：
如图②，已知△ABC是边长为4的等边三角形，以BC为边向外作等边△BCD，P为△ABC内一点，将线段CP绕点C逆时针旋转60°，P的对应点为Q．3
（1）求证：△DCQ≌△BCP
（2）求PA+PB+PC的最小值．
实际应用：
如图③，某货运场为一个矩形场地ABCD，其中AB=500米，AD=800米，顶点A、D为两个出口，现在想在货运广场内建一个货物堆放平台P，在BC边上（含B、C两点）开一个货物入口M，并修建三条专用车道PA、PD、PM．若修建每米专用车道的费用为10000元，当M，P建在何处时，修建专用车道的费用最少？最少费用为多少？
发布：2025/5/25 22:30:2组卷：514引用：2难度：0.1 -
2．如图，在平面直角坐标系中，矩形ABCO的边OC与x轴重合，OA与y轴重合，BC=2，D是OC上一点，且OD，DC的长是一元二次方程x2-5x+4=0的两个根（OD＞DC）．
（1）求线段OD，OC，AD的长；
（2）在线段AB上有一动点P（不与A、B重合），点P从点A出发，以每秒1个单位长度的速度沿AB方向匀速运动，到终点B停止，设运动的时间为t秒，过P点作PE∥BD交AD于E，PF∥AD交BD于F，求四边形DEPF的面积S与时间t的函数关系式；
（3）在（2）的条件下，在点P运动的过程中，x轴上是否存在点Q，使以A、D、P、Q为顶点的四边形是菱形？若存在，请直接写出点Q的坐标，若不存在，请说明理由．
发布：2025/5/25 22:30:2组卷：107引用：1难度：0.3 -
3．折纸是同学们喜欢的手工活动之一，通过折纸我们既可以得到许多美丽的图形．同时纸的过程还蕴含着丰富的数学知识．
折纸1：如图1，将正方形ABCD沿BE对折，使点A落在点A'，连接A'C，若∠DEA'=50°，则∠BA'C=．
折纸2：请用一个正方形纸片折出一个30°的角（不借助任何工具），在给出的正方形图形（图2）中画出你的折叠方法，并说明理由．
折纸3：如图3，操作一；将边长为4的正方形片ABCD对折，使点B、C分别与点A，D重合，再展开得到折痕EF；操作：将正方形ABCD沿着AF折叠，使得点D落在点D'处；操作三：正方形纸片沿着FD'折叠再展开，折痕FD'与边BC于点P，求线段BP的长度．
综合应用：如图4，在矩形ABCD中，AB=6，BC=8，点P为BC上的一点（不与B点重合，可以与C点重合），将△ABP沿着AP折叠，点B的对应点为B'，B'落在矩形的内部，连结B'A，B'D，当△B'AD为等腰三角形时，求△B'AD的面积．
发布：2025/5/25 22:30:2组卷：342引用：1难度：0.2
