如图，第一象限内半径为2的⊙C与y轴相切于点A，作直径AD，过点D作⊙C的切线l交x轴于点B，P为直线l上一动点，已知直线PA的解析式为：y=kx+3．
（1）设点P的纵坐标为p,写出p随k变化的函数关系式．
（2）设⊙C与PA交于点M，与AB交于点N，则不论动点P处于直线l上（除点B以外）的什么位置时，都有△AMN∽△ABP．请你对于点P处于图中位置时的两三角形相似给予证明；
（3）是否存在使△AMN的面积等于3225的k值？若存在，请求出符合的k值；若不存在，请说明理由．
32
25
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：667引用：10难度：0.5
相似题
-
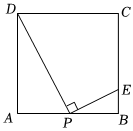1．如图，在边长为10cm的正方形ABCD中，P为AB边上任意一点（P不与A、B两点重合），连接DP，过点P作PE⊥DP，垂足为P，交BC于点E，则BE的最大长度为 cm.发布：2025/6/19 6:0:1组卷：884引用：59难度：0.7 -
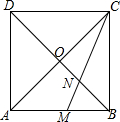2．如图，正方形ABCD的对角线AC与BD相交于点O，∠ACB的角平分线分别交AB、BD于M、N两点．若AM=2，则线段ON的长为（ ）发布：2025/6/19 6:0:1组卷：10870引用：93难度：0.5 -
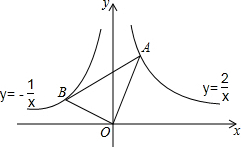3．如图，在x轴的上方，直角∠BOA绕原点O按顺时针方向旋转，若∠BOA的两边分别与函数y=-、y=1x的图象交于B、A两点，则∠OAB的大小的变化趋势为（ ）2x发布：2025/6/19 6:0:1组卷：5062引用：71难度：0.9
