如图1，点P为直线AB、CD内部一点，连接PE、PF，∠P=∠BEP+∠PFD．
（1）求证：AB∥CD；
（2）如图2，点G为AB上一点，连接GP并延长交CD于点H，若∠PHF=∠EPF，过点G作GK⊥EP于点K，求证：∠PFH+∠PGK=90°．
（3）如图3，在（2）的条件下，PQ平分∠EPF，连接QH，12∠FPH=∠PFH+∠EPQ，当∠PHQ=2∠GPE时，∠QHC=∠QPF-10°，求∠Q的度数．
1
2
【考点】平行线的判定与性质．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/6 8:0:9组卷：115引用：2难度：0.6
相似题
-
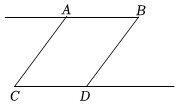1．如图，已知AC∥BD，请添加一个条件，使得AB∥CD，则添加的条件是．发布：2025/6/20 11:0:1组卷：83引用：2难度：0.8 -
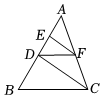2．如图，在三角形ABC中，点D，E在边AB上，点F在边AC上，连接CD，DF，EF，若DF∥BC，则添加下列条件不能判定EF∥CD的是（ ）发布：2025/6/20 11:0:1组卷：44引用：1难度：0.6 -
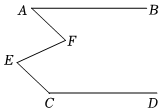3．在期末复习阶段，老师给同学们留了这样一道题：如图，已知∠A+∠DCE=180°，∠AFE=∠CEF，AF=CE，试说明AB∥CD．
（1）以下是小鹿给出的解题过程，请补全过程和依据：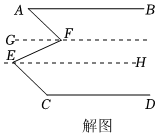
解：如解图，分别过点F，E作FG∥EH∥AB，
因为FG∥EH，
所以∠EFG=∠FEH（ ），
又因为∠AFE=∠CEF，且∠AFG+∠EFG=∠AFE，∠FEH+∠CEH=∠CEF，
所以∠CEH=．
因为AB∥FG，
所以 =∠AFG，
所以∠CEH=∠A，
又因为∠A+∠DCE=180°，
所以∠CEH+∠DCE=180°，
所以CD∥EH，
因为EH∥AB，
所以AB∥CD（ ）；
（2）小万发现这道题不止有一种做法，请你用其他方法来说明AB∥CD．发布：2025/6/20 11:0:1组卷：24引用：1难度：0.6
