【了解概念】
如图1，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，连接CE，连接BD并延长与CE交于点F，那么将∠BFC叫做△ABC和△ADE的底联角．
【探究归纳】
（1）两个等腰三角形的底联角与这两个等腰三角形的顶角有怎样的数量关系？请用文字语言写出结论．
【拓展提升】
运用（1）中的结论解决问题：
（2）如图2，AB=AC，AD=AE，∠BAC=DAE=90°，∠DCE=62°，求∠BDC的度数；
（3）如图3，在四边形ABCD中，AB=6，BC=4，CD=5，点O为四边形ABCD内一点．且OA=OB，OC=OD，∠AOB=∠COD=90°，求AD的长．
【考点】四边形综合题．
【答案】（1）两个等腰三角形的底联角等于这两个等腰三角形的顶角，理由见解答；
（2）∠BDC=152°或∠BDC=28°；
（3）AD的长为3．
（2）∠BDC=152°或∠BDC=28°；
（3）AD的长为3
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/4 1:0:8组卷：1065引用：4难度：0.3
相似题
-
1．（1）【问题发现】
如图1，在Rt△ABC中，AB=AC，∠BAC=90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为．
（2）【拓展探究】
在（1）的条件下，如果正方形CDEF绕点C旋转，请判断线段BE与AF的数量关系，并就图2的情形说明理由．
（3）【问题解决】
当AB=AC=2，且第（2）中的正方形CDEF旋转到B，E，F三点共线时，请直接写出线段AF的长．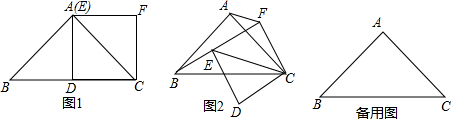
发布：2025/5/24 21:30:1组卷：328引用：4难度：0.2 -
2．如图1，在矩形ABCD中，AB=5，BC=8，点E，F分别为AB，CD的中点．
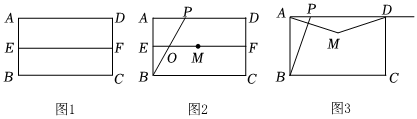
（1）四边形AEFD是哪种特殊的平行四边形？为什么？
（2）如图2，点P是边AD上一点，BP交EF于点O，点A关于BP的对称点为点M，当点M落在线段EF上时，请说明PB=2OM；
（3）如图3，若点P是射线AD上一个动点，点A关于BP的对称点为点M，连接AM，DM，当△AMD是等腰三角形时，请先直接写出所有符合条件的线段AP的长，再任选1种情况说明理由．发布：2025/5/24 23:30:2组卷：60引用：2难度：0.2 -
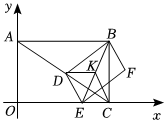3．在平面直角坐标系中，O为原点，四边形ABCO是矩形，点A（0，2），C（2，0），点D是对角线AC上一点（不与A、C重合），连接BD，作DE⊥BD，交x轴于点E，以线段DE、DB为邻边作矩形BDEF，连接BE，K为BE的中点，分别连接DK，CK．3
（1）直接写出点B的坐标；
（2）求证：DK=CK；
（3）是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD的长；若不存在，请说明理由．发布：2025/5/24 22:30:1组卷：13引用：1难度：0.4
