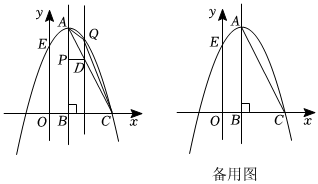
如图，在平面直角坐标系中，Rt△ABC的边BC在x轴上，∠ABC=90°，以A为顶点的抛物线y=-x2+bx+c经过点C（3，0），交y轴于点E（0，3），动点P在对称轴上．
（1）求抛物线的解析式．
（2）若点P从A点出发，沿A→B方向以1个单位长度/秒的速度匀速运动到点B停止，设运动时间为t秒，过点P作PD⊥AB交AC于点D，过点D且平行于y轴的直线l交抛物线于点Q，连接AQ，CQ，当t为何值时，△ACQ的面积最大？最大值是多少？
（3）抛物线上是否存在点M，使得以点P，M，E，C为顶点的四边形是平行四边形？若存在，请求出点M的坐标；若不存在，请说明理由．
【考点】二次函数综合题．
【答案】（1）y=-x2+2x+3；
（2）当t=2时，△ACQ的面积最大，最大值为1；
（3）存在点M，使得以点P，M，E，C为顶点的四边形是平行四边形，点M的坐标为（2，3），（-2，-5）或（4，-5）．
（2）当t=2时，△ACQ的面积最大，最大值为1；
（3）存在点M，使得以点P，M，E，C为顶点的四边形是平行四边形，点M的坐标为（2，3），（-2，-5）或（4，-5）．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 8:0:10组卷：63引用：1难度：0.2
相似题
-
1．在平面直角坐标系xOy中，二次函数y=ax2+bx+4（a＜0）的图象与x轴交于点A（-2，0）和点B（4，0），与y轴交于点C，直线BC与对称轴于点D．
（1）求二次函数的解析式．
（2）若抛物线y=ax2+bx+4（a＜0）的对称轴上有一点M，以O、C、D、M四点为顶点的四边形是平行四边形时，求点M的坐标．
（3）将抛物线y=ax2+bx+4（a＜0）向右平移2个单位得到新抛物线，新抛物线与原抛物线交于点E，点F是新抛物线的对称轴上的一点，点G是坐标平面内一点，当以D、E、F、G四点为顶点的四边形是菱形时，求点F的坐标．发布：2025/5/23 23:30:1组卷：634引用：3难度：0.3 -
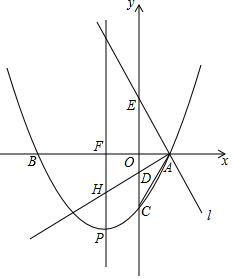2．如图，抛物线y=ax2+bx+c与x轴交于A（，0），B两点（点B在点A的左侧），与y轴交于点C，且OB=3OA=3OC，∠OAC的平分线AD交y轴于点D，过点A且垂直于AD的直线l交y轴于点E，点P是x轴下方抛物线上的一个动点，过点P作PF⊥x轴，垂足为F，交直线AD于点H．3
（1）求抛物线的解析式；
（2）设点P的横坐标为m,当FH=HP时，求m的值；
（3）当直线PF为抛物线的对称轴时，以点H为圆心，HC为半径作⊙H，点Q为⊙H上的一个动点，求12AQ+EQ的最小值．14发布：2025/5/24 0:0:1组卷：3204引用：2难度：0.3 -
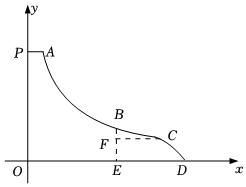3．如图，是某水上乐园为亲子游乐区新设滑梯的示意图，其中线段PA是竖直高度为6米的平台，PO垂直于水平面，滑道分为两部分，其中AB段是双曲线y=的一部分，BCD段是抛物线的一部分，两滑道的连接点B为抛物线的顶点，且B点的竖直高度为2米，滑道与水平面的交点D距PO的水平距离为7米，以点O为坐标原点建立平面直角坐标系，滑道上点的竖直高度为y,距直线PO的水平距离为x.10x
（1）请求出滑道BCD段y与x之间的函数关系式；
（2）当滑行者滑到C点时，距地面的距离为1米，求滑行者此时距滑道起点A的水平距离；
（3）在建模实验中发现，为保证滑行者的安全，滑道BCD落地点D与最高点B连线与水平面夹角应不大于45°，且由于实际场地限制，≥OPOD，求OD长度的取值范围．12发布：2025/5/23 23:0:1组卷：271引用：2难度：0.2
