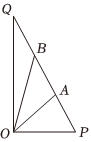
为打造美好生态校园，缓解学生的学习压力，培养学生的责任和担当意识，某校北校区拟开设饲养动物的课程．校园内有一块空地△OPQ（如图所示），其中OP=30m,OQ=303m,∠POQ=π2．学校拟在空地中间规划动物休息区域△OAB，活动区域△OPA，且∠AOB=π6，现需要在△OPB的周围安装防护网．
（1）当PA=15m时，求防护网的总长度；
（2）为了节约成本投入，要求动物休息区域△OAB尽可能小，问如何规划，能让△OAB的面积最小？最小面积是多少？
3
π
2
π
6
【考点】解三角形．
【答案】（1）90m；（2）当∠AOP=时，能让△OAB的面积最小，最小面积是675（2-）m2．
π
12
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/2 8:0:9组卷：14引用：1难度：0.4
相似题
-
1．在①
，②2a-c=2bcosC，③（a-b）（a+b）=（a-c）c这三个条件中任选一个，补充在下面的问题中，并解答该问题．3（a-bcosC）=csinB
在△ABC中，内角A，B，C的对边分别是a,b,c,且满足 _____，．b=23
（1）若a+c=4，求△ABC的面积；
（2）求△ABC周长l的取值范围．发布：2024/12/29 13:0:1组卷：291引用：4难度：0.5 -
2．已知灯塔A在海洋观察站C的北偏东65°，距离海洋观察站C的距离为akm,灯塔B在海洋观察站C的南偏东55°，距离海洋观察站C的距离为3akm,则灯塔A与灯塔B的距离为（ ）
发布：2024/12/30 4:0:3组卷：50引用：3难度：0.7 -
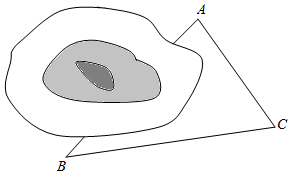3．如图，在铁路建设中，需要确定隧道两端的距离（单位：百米），已测得隧道两端点A，B到某一点C的距离分别为5和8，∠ACB=60°，则A，B之间的距离为（ ）发布：2024/12/29 13:0:1组卷：295引用：5难度：0.7
