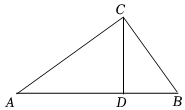
在Rt△ABC中，∠ACB=90°，CD是斜边AB边上的高．求证∠ACD=∠B．
证明：在Rt△ABC中，∠A+∠B=90°（根据是 直角三角形两锐角互余直角三角形两锐角互余）．
在Rt△ACD中，∠A+∠ACDACD=90°（根据是 直角三角形两锐角互余直角三角形两锐角互余），
∴∠ACD=∠B（根据是 等量代换等量代换）．
【考点】直角三角形的性质．
【答案】直角三角形两锐角互余；ACD；直角三角形两锐角互余；等量代换
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/13 15:0:8组卷：9引用：1难度：0.7
相似题
-
1．已知：如图，DG⊥BC，AC⊥BC，EF⊥AB，∠1=∠2．求证：CD⊥AB．将证明过程补充完整．
证明：∵DG⊥BC，AC⊥BC
∴∠DGB=∠ACB=90°（）
∴DG∥AC（）
∴∠2=∠DCA（）
∵∠1=∠2（）
∴∠1=∠DCA（）
∴EF∥CD（）
∴∠AEF=∠ADC（）
∵EF⊥AB
∴∠AEF=90°（）
∴∠ADC=90°，即CD⊥AB．发布：2025/6/21 11:30:1组卷：420引用：2难度：0.7 -
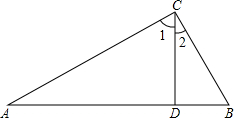
2．如图，∠ACB=90°，CD⊥AB，垂足为D，下列结论错误的是（ ）
发布：2025/6/21 12:0:1组卷：5129引用：27难度：0.9 -
3．在直角三角形ABC中，∠A：∠B：∠C=2：m：4，则m的值是（ ）
发布：2025/6/21 13:0:29组卷：2927引用：29难度：0.8
