 《九章算术》中的“方田章”论述了三角形面积的求法:“圭田术曰,半广以乘正广”,就是说:“三角形的面积=底×高÷2”,我国著名的数学家秦九韶在《数书九章》中也提出了“三斜求积术”,即可以利用三角形的三条边长来求取三角形面积,用现代式子可表示为:S=14[a2b2-(a2+b2-c22)2](其中a、b、c为三角形的三条边长,S为三角形的面积).如图,在▱ABCD中,已知AB=6,AD=3,对角线BD=5,则▱ABCD的面积为( )
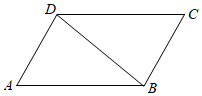
《九章算术》中的“方田章”论述了三角形面积的求法:“圭田术曰,半广以乘正广”,就是说:“三角形的面积=底×高÷2”,我国著名的数学家秦九韶在《数书九章》中也提出了“三斜求积术”,即可以利用三角形的三条边长来求取三角形面积,用现代式子可表示为:S=14[a2b2-(a2+b2-c22)2](其中a、b、c为三角形的三条边长,S为三角形的面积).如图,在▱ABCD中,已知AB=6,AD=3,对角线BD=5,则▱ABCD的面积为( )
1
4
[
a
2
b
2
-
(
a
2
+
b
2
-
c
2
2
)
2
]
6
3
5
【答案】B
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/5/27 14:0:0组卷:53引用:4难度:0.7
相似题
-
 1.如图,在▱ABCD中,∠BAD,∠ADC的平分线AF,DE分别与线段BC交于点F,E,AF与DE交于点G.
1.如图,在▱ABCD中,∠BAD,∠ADC的平分线AF,DE分别与线段BC交于点F,E,AF与DE交于点G.
(1)求证:AF⊥DE,BF=CE.
(2)若AD=10,AB=6,AF=8,求DE的长度.发布:2025/5/24 12:30:1组卷:1612引用:6难度:0.6 -
 2.如图,在▱ABCD中,E为CD的中点,连接BE并延长,交AD的延长线于点F.
2.如图,在▱ABCD中,E为CD的中点,连接BE并延长,交AD的延长线于点F.
(1)求证:△BCE≌△FDE;
(2)若BC=3,求AF的长.发布:2025/5/24 9:30:2组卷:909引用:4难度:0.5 -
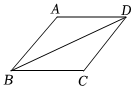 3.如图,在▱ABCD中,AB=BC=6,对角线BD=10,则▱ABCD的面积为 .发布:2025/5/24 14:0:2组卷:54引用:1难度:0.5
3.如图,在▱ABCD中,AB=BC=6,对角线BD=10,则▱ABCD的面积为 .发布:2025/5/24 14:0:2组卷:54引用:1难度:0.5


