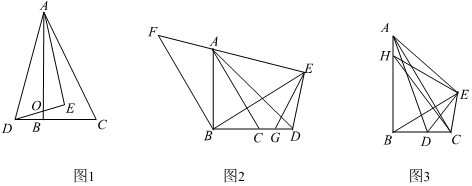
如图，在Rt△ABC中，∠ABC=90°，∠BAC=30°，点D在直线BC上运动，连接AD，以AD为斜边在直线AD的右侧作Rt△ADE，其中∠AED=90°，∠DAE=30°．
（1）如图1，点D运动到点B的左侧时，DE与AB相交于点O，当AO平分∠DAE时，若DC=4，求AD的长；
（2）如图2，点D沿射线BC方向运动过程中，当BD=AB时，连接BE，过点B作BF⊥BE交EA的延长线于点F，取CD的中点G，连接EG．猜测BG与GE的数量关系，并证明你的猜想；
（3）如图3，点D沿射线CB方向运动过程中，连接BE，将线段BE绕点E顺时针方向旋转60°，得到线段EH，连接AH、CH，若AB=3，当CH+12AH取得最小值时，请直接写出△BCE的面积．
1
2
【考点】几何变换综合题．
【答案】（1）2；（2）BG=EG，证明见解答；（3）．
6
3
4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/31 8:0:9组卷：319引用：2难度：0.4
相似题
-
1．如图①，在Rt△ABC中，∠B=90°，AB=5，BC=12，CD=5，DE∥AB．将△EDC绕点C按顺时针方向旋转，记旋转角为α．
（1）①当α=0°时，=；②当α=180°时，AEBD=．AEBD
（2）试判断：当0≤α≤360°时，的大小有无变化？请仅就图②的情形给出证明．AEBD
（3）当△EDC旋转到A，D，E三点共线时，直接写出线段BD的长．
发布：2025/5/23 20:0:1组卷：194引用：3难度：0.3 -
2．如图，在平面直角坐标系中有Rt△ABO，∠BAO=90°，∠ABO=30°，B（-8，0）．将三角形ABO绕着点O顺时针方向旋转，旋转后点A与A1，点B与B1相重合．
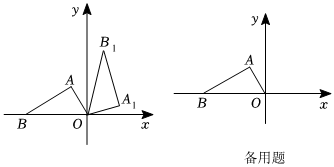
（1）当旋转角为60°时，求点B1的坐标；
（2）当点B1落在BA的延长线上时，求点B1的坐标．
（3）若点E为AB的中点，求EB1的最大值和最小值．（直接写出结果即可）发布：2025/5/23 18:0:1组卷：688引用：5难度：0.1 -
3．如图1，在△ABC中，∠BAC=90°，AB=AC=4，点E为边AC上一点，以AE为斜边，在△ABC外，作△ADE，使得∠ADE=90°，且DE=DA．现将△ADE绕点A逆时针旋转，旋转角为α（0°＜α＜90°），连接BE．
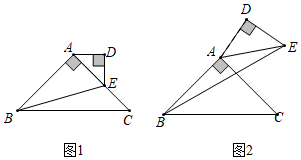
（1）如图2，当α=15°且BE∥AD时，求BE的长；
（2）连接CE，设CE的中点为点F，AE的中点为点H，连接DF，直线DF与线段BE交于点G，连接GH．
①求证：DF⊥BE；
②探索线段GH，GD，GE之间的数量关系．发布：2025/5/23 22:0:2组卷：430引用：2难度：0.2
