阅读材料：
已知a2+4b2-2a-4b+2=0，求a,b的值．
解：∵a2+4b2-2a-4b+2=0，
∴a2-2a+1+4b2-4b+1=-2+1+1，
∴（a-1）2+（2b-1）2=0，
∴a-1=0，2b-1=0，
∴a=1，b=12．
参照上面材料，解决下列问题：
（1）【应用】若a2+2ab+2b2+4b+4=0，求ba的值．
（2）【拓展】a、b、c是△ABC的三边，且有a2+b2=4a+10b-29．
①若c为奇数，求c的值．
②直接写出这个三角形的周长取值范围．
1
2
【答案】（1）4；
（2）大于10且小于14．
（2）大于10且小于14．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/11 8:0:9组卷：152引用：1难度：0.5
相似题
-
1．我们知道：x2-6x=（x2-6x+9）-9=（x-3）2-9；-x2+10x=-（x2-10x+25）+25=-（x-5）2+25，这一种方法称为配方法，利用配方法请解以下各题：
（1）按上面材料提示的方法填空：a2-4a==．-a2+12a==．
（2）探究：当a取不同的实数时在得到的代数式a2-4a的值中是否存在最小值？请说明理由．
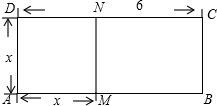
（3）应用：如图．已知线段AB=6，M是AB上的一个动点，设AM=x,以AM为一边作正方形AMND，再以MB、MN为一组邻边作长方形MBCN．问：当点M在AB上运动时，长方形MBCN的面积是否存在最大值？若存在，请求出这个最大值；否则请说明理由．发布：2025/6/21 14:0:1组卷：723引用：25难度：0.7 -
2．阅读材料：数学课上，吴老师在求代数式x2-4x+5的最小值时，利用公式a2±2ab+b2=（a±b）2，对式子作如下变形：x2-4x+5=x2-4x+4+1=（x-2）2+1，
因为（x-2）2≥0，
所以（x-2）2+1≥1，
当x=2时，（x-2）2+1=1，
因此（x-2）2+1有最小值1，即x2-4x+5的最小值为1．
通过阅读，解下列问题：
（1）代数式x2+6x+12的最小值为；
（2）求代数式-x2+2x+9的最大或最小值；
（3）试比较代数式3x2-2x与2x2+3x-7的大小，并说明理由．发布：2025/6/21 14:0:1组卷：2031引用：6难度：0.3 -
3．把a2+b2+c2+ab+bc+ac配成三项完全平方式相加．
发布：2025/6/21 14:30:1组卷：69引用：2难度：0.7
