在△ABC中，内角A、B、C所对的边分别是a、b、c,2sinA+11-2cosA=sin2C1+cos2C．
（1）若B=π6，求C；
（2）若B∈[π6，π4），求cb的取值范围．
2
sin
A
+
1
1
-
2
cos
A
=
sin
2
C
1
+
cos
2
C
B
=
π
6
B
∈
[
π
6
，
π
4
）
c
b
【答案】（1）；
（2）．
C
=
5
π
12
（2）
（
2
，
6
+
2
2
]
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/11 8:0:9组卷：414引用：4难度：0.5
相似题
-
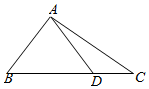1．如图，在△ABC中，已知B=45°，D是BC边上的一点，AD=4，AC=2，DC=2．7
（1）求cos∠ADC；
（2）求AB．发布：2024/12/29 12:0:2组卷：111引用：5难度：0.5 -
2．在△ABC中，角所对的边分别为a,b,c,给出下列四个命题中，其中正确的命题为（ ）
发布：2024/12/29 12:0:2组卷：188引用：14难度：0.6 -
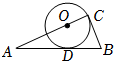3．如图，在Rt△ABC中，∠C=90°，O是边AC上一点，直线AB与圆O相切，切点为斜边的中点D，直线BC与圆O相切，若圆O的面积为π，则△ABC的面积为（ ）发布：2025/1/28 8:0:2组卷：41引用：1难度：0.7
