某中学七年级数学课外兴趣小组在探究：“n边形（n＞3）共有多少条对角线”这一问题时，设计了如下表格，请在表格中的横线上填上相应的结果：

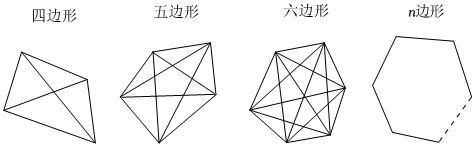
多边形的边数 4 5 6 ⃯ n

从多边形的一个顶点出发 1 2
3
3
…
n-3
n-3

多边形对角线的总条数 2
5
5

9
9
…
n
（
n
-
3
）
2
n
（
n
-
3
）
2

应用得到的结果解决以下问题：
①求十二边形有多少条对角线？
②过多边形的一个顶点的所有对角线条数与这些对角线分多边形所得的三角形个数的和可能为2023吗？若能，请求出这个多边形的边数；若不能，请说明理由．

【答案】3；n-3；5；9；

（

）

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/5/23 8:0:8组卷：261引用：2难度：0.6

相似题

2．欧拉是18世纪瑞士著名的数学家，他发现不论什么形状的凸多面体．其顶点数（V）、面数（F）、棱数（E）之间存在的一个固定的关系式，被称为多面体欧拉定理．请你观察下列几种简单多面体模型，解答下列问题．
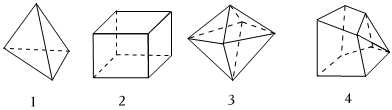
（1）【公式发现】根据上面的多面体模型，完成表格中的空格：

多面体编号顶点数（V）面数（F）棱数（E）

1 4 4 6

2 8 6 12

3 6 8 12

4 9 8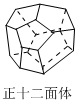

你发现顶点数（V）、面数（F）和棱数（E）之间存在的关系式是
．
（2）[公式运用]如图请计算正十二面体的顶点数和棱数．
（3）[公式综合]已知某个玻璃饰品的外形是简单多面体，它的外表面是由三角形和六边形两种多边形排接而成，且有18个顶点，每个顶点处都有4条棱，设该多面体外表面三角形的个数为m个，六边形的个数为n个，求m+n的值．
（4）[定理应用]有一种足球是由数块黑白相间的牛皮缝制而成，黑皮为正五边形，白皮为正六边形，且边长都相等，请利用欧拉公式分别求出正五边形、正六边形个数．

发布：2025/5/24 15:30:1组卷：143引用：1难度：0.3