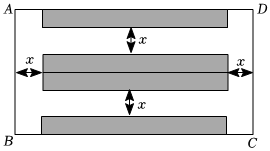
社区利用一块矩形空地ABCD建了一个小型停车场，其布局如图所示．已知AD=52m,AB=28m,阴影部分设计为停车位，要铺花砖，其余部分均为宽度为x米的道路．已知铺花砖的面积为640m2．
（1）求道路的宽是多少米？
（2）该停车场共有车位50个，据调查分析，当每个车位的月租金为200元时，可全部租出；若每个车位的月租金每上涨5元，就会少租出1个车位．当每个车位的月租金上涨多少元时，停车场的月租金收入为10125元？
【考点】一元二次方程的应用．
【答案】（1）道路的宽为6米；（2）每个车位的月租金上涨25元时，停车场的月租金收入为10125元．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/27 20:0:2组卷：2246引用：14难度：0.5
相似题
-
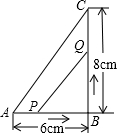1．如图，在△ABC中，∠B=90°，点P从点A开始沿AB边向点B以1cm/秒的速度移动，点Q从点B开始沿BC边向点C以2cm/秒的速度移动．
（1）如果P、Q分别从A、B同时出发，几秒后△PBQ是等腰直角三角形？
（2）如果P、Q分别从A、B同时出发，几秒后△PBQ的面积等于3cm2？
（3）如果P、Q分别从A、B同时出发，四边形APQC的面积是△ABC面积的三分之二？发布：2025/1/20 8:0:1组卷：125引用：1难度：0.5 -
2．如图，矩形ABCD中，AB=8cm,BC=6cm,点M从点A出发，沿着AB→BC的方向以4cm/s的速度向终点C匀速运动；点N从点B出发，沿着BC→CD的方向以3cm/s的速度向终点D匀速运动；点M，N同时出发，当M，N中任何一个点到达终点时，另一个点同时停止运动，点M运动时间为t（s），连接MN，△BMN的面积为S（cm2）．
（1）求S关于t的函数解析式，并直接写出自变量t的取值范围；
（2）△BMN的面积可以是矩形ABCD面积的吗？如能，求出相应的t值，若不能，请说明理由．14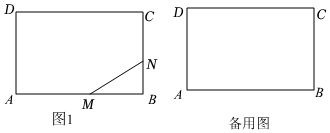
发布：2025/1/13 8:0:2组卷：260引用：4难度：0.6 -
3．如图，在△ABC中，∠C=90°，AB=10cm,AC=8cm,点P，Q同时由A，C两点出发，分别沿AC，CB方向移动，它们的
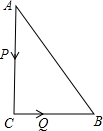速度都是2cm/s.
（1）设经过t秒后，那么在△PCQ中，此时线段，线段CQ长为cm,PC长为cm.
（2）经过几秒，P，Q相距cm？210发布：2025/1/24 8:0:2组卷：205引用：6难度：0.3
